Il n’aurait pas un peu de mal parfois python ?
Résultat d’une addition simple avec ipython (python 2.7.9).
Il n’aurait pas un peu de mal parfois python ?
Résultat d’une addition simple avec ipython (python 2.7.9).
[include-mastodon-feed instance="piaille.fr" account="UnColmarien"]
Nous avons remarqué que vous n'utilisez PAS de bloqueur de publicités !
Pour préserver votre cerveau, et nettoyer le web nous vous conseillons l'installation d'un bloqueur.
uBlock Origin est l'une des extensions firefox la plus respectueuse de votre vie privée, n'hésitez pas à l'installer.
| L | M | M | J | V | S | D |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | |||||

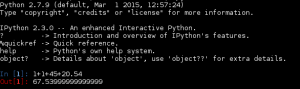
Tout les nombres « décimaux » de sont pas encodables en nombre flottant binaires.
Ici, python encode en « flottant binaire » (probablement du IEEE754 binary64) l’expression décimale tapée sur la ligne de commande, puis affiche en retour, une représentation décimale proche de ce qui est réellement encodé, tout en garantissant un nombre maximal de « digits ».
Car contrairement a ce que j’ai précédemment écrit, il est possible de représenter, de façon exacte, en décimal, tout nombre représenté de façon exacte en « flottant binaire ». Mais cela peut nécessiter un grand nombre de « digits »:
Exemple de conversions :
Conversion de: -4.7233169650e+4
Signum bit ‘-‘.
–> -0x###p#
Reste: 4.7233169650e+4
Choix de la base : 2^15 = 32768 –> p15
–> -0x1.###p15
Reste: 14465.16965
Décomposition:
> 2^14 = 16384 –> 0 »
> 2^13 = 8192 –> 1 (reste 6273.16965)
> 2^12 = 4096 –> 1 (reste 2177.16965)
> 2^11 = 2048 –> 1 (reste 129.16965)
> 2^10 = 1024 –> 0 »
> 2^9 = 512 –> 0 »
> 2^8 = 256 –> 0 »
> 2^7 = 128 –> 1 (reste 1.16965)
> 2^6 = 64 –> 0 »
> 2^5 = 32 –> 0 »
> 2^4 = 16 –> 0 »
> 2^3 = 8 –> 0 »
> 2^2 = 4 –> 0 »
> 2^1 = 2 –> 0 »
> 2^0 = 1 –> 1 (reste 0.16965)
> 2^-1 = 0.5 –> 0 »
> 2^-2 = 0.25 –> 0 »
> 2^-3 = 0.125 –> 1 (reste 0.04465)
> 2^-4 = 0.0625 –> 0 »
> 2^-5 = 0.03125 –> 1 (reste 0.0134)
> 2^-5 = 0.015625 –> 0 »
> 2^-7 = 0.0078125 –> 1 (reste 0.0055875)
> 2^-8 = 0.00390625 –> 1 (reste 0.00168125)
> 2^-9 = 0.001953125 –> 0 »
> 2^-10 = 0.0009765625 –> 1 (reste 0.0007046875)
> 2^-11 = 0.00048828125 –> 1 (reste 0.00021640625)
> 2^-12 = 0.000244140625 –> 0 »
> 2^-13 = 0.0001220703125 –> 1 (reste 0.0000943359375)
> 2^-14 = 0.00006103515625 –> 1 (reste 0.00003330078125)
> 2^-15 = 0.000030517578125 –> 1 (reste 0.000002783203125)
> 2^-16 = 0.0000152587890625 –> 0 »
> 2^-17 = 0.00000762939453125 –> 0 »
En binaire : 0111 0001 0000 0010 0101 0110 1101 1100(2)
En hexa = 7 1 0 2 5 6 D C
–> -0x1.710256DCp15
Certes … mais ma calculette solaire offerte par ma banque elle fait pas l’erreur elle !