Les 10 ans de Cocotb était l’occasion rêvée pour sortir la version 1.8 😉
Et voila, ça fait 10 ans que Cocotb existe. On remercie toute l’équipe du projet qui a ainsi ré-enchanté la validation VHDL/Verilog.
Longue vie à Cocotb \o/
Identification des bitstreams de la série 7 avec usr_access2
Le processus de synthèse/placement/routage/bitstream prenant beaucoup de temps, on est amené à faire d’autres activité pendant le traitement. Ce «switch» de tâche nous amène à faire des erreurs fréquentes de version de bitstream au moment de la configuration du FPGA.
Il est fréquent de passer des heures voir des jours sur un bug qui n’en était finalement pas un puisque nous n’avions pas mis à jour la version du bitstream.
Pour éviter ce problème il faut pouvoir lire la version du bitstream généré de manière à s’assurer qu’on travail bien avec la bonne.
C’est exactement l’objet de la macro «usr_access» des FPGA de la série 7 de Xilinx.
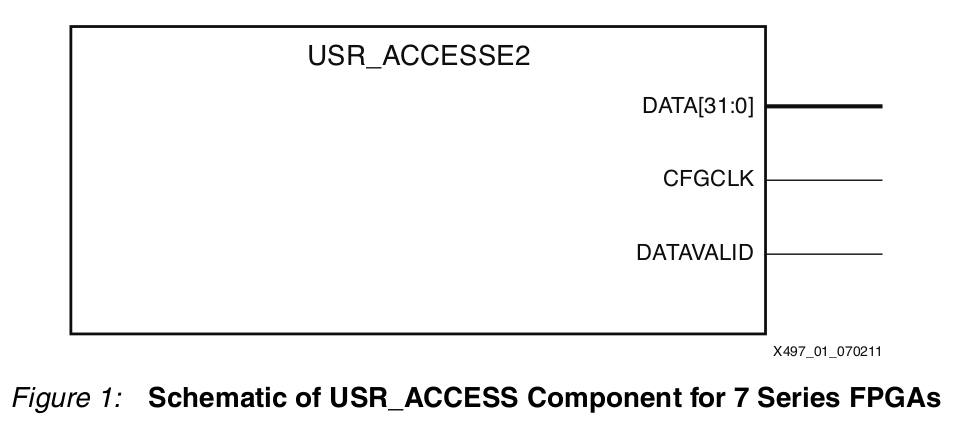
Cette macro est appelée de la manière suivante en VHDL :
library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
use IEEE.numeric_std.all;
Entity usr_accesse2 is
port
(
CFGCLK : out std_logic;
DATA : out std_logic_vector(31 downto 0);
DATAVALID : out std_logic
);
end entity;
Architecture usr_accesse2_1 of usr_accesse2 is
begin
CFGCLK <= '1';
DATA <= x"00000E0F";
DATAVALID <= '1';
end architecture usr_accesse2_1;
Et la valeurs de la sortie «DATA» est ré-inscriptible jusqu’à la génération du bitstream avec l’option -g USR_ACCESS.
Pour y mettre la date et l’heure on utilisera l’option timestamp dans le menu tools->edit device property.
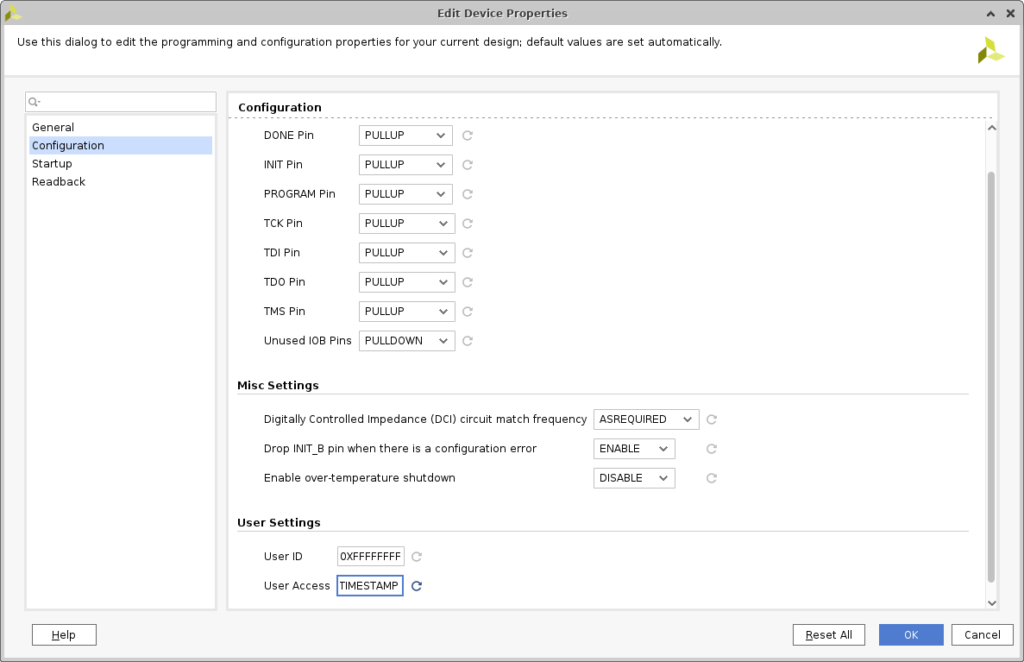
Cette action à pour effet d’ajouter la commande suivante dans le xdc :
set_property BITSTREAM.CONFIG.USR_ACCESS TIMESTAMP [current_design]Mais elle ne met pas la date chez moi pour le moment 🙁
Un timeout dans cocotb
Avec Cocotb nous avons parfois des coroutines qui sont susceptible de rester «coincées» dans une boucle d’attente infinie. Si l’on y prête pas garde, on a vite fait de remplir son disque dur de traces totalement inutile.
# Une coroutine qui attend bien trop longtemps
async def too_long_coroutine(self):
await Timer(1, units="sec")Pour éviter ce problème, l’idéal serait de pouvoir ajouter un «timeout» à l’appel de la coroutine susceptible de bloquer.
Ça tombe bien, cocotb a prévu un trigger pour ça : with_timeout()
from cocotb.triggers import with_timeout
await with_timeout(testcls.too_long_coroutine(), 100, "ns")Sauf que python n’a pas trop l’air d’accord pour exécuter notre coroutine comme un trigger.
TypeError: All triggers must be instances of Trigger! Got: coroutineC’est dommage, on perd beaucoup de l’intérêt de ce trigger !
La solution donnée par marlonjames est d’«empaquetter» la coroutine dans la fonction start_soon() comme ceci :
await with_timeout(
cocotb.start_soon(testcls.too_long_coroutine()),
100, "ns")De cette manière, le test s’interromps sur une levé d’interruption SimTimeoutError et le test est marqué FAIL sans ruiner notre disque dur.
raise cocotb.result.SimTimeoutError
cocotb.result.SimTimeoutErrorInstallation des outils libres de simulations pour windows
C’est une réalité aujourd’hui, il y a encore beaucoup d’entreprises qui tournent exclusivement avec le système d’exploitation de Microsoft.
L’environnement Microsoft n’est pas idéal pour faire fonctionner les outils de simulations libre, mais c’est tout de même possible.
Voyons comment faire pour installer Yosys, GHDL, smtbmc, gtkwave et autres outils classique dans le monde de la simulation libre sur Windows 10 Famille.
MSYS2
MSYS2 est un environnement/shell de développement open-source pour windows. Pour l’installer il suffit de se rendre sur la page officiel du projet et de télécharger l’installeur (83.5Mo).
Le répertoire par défaut «c:/msys64» convient très bien et installera un raccourci dans le menu de windows. N’oubliez pas de désactiver votre antivirus avant de lancer l’installation, sinon il aura peur de gpg et vous empêchera de l’installer correctement !
Une fois installé, la console se lance. Nous allons commencer par mettre à jours MSYS avec pacman :
$ pacman -SyuLa commande aura pour effet de fermer la fenêtre de console, qu’il faudra réouvrir pour lancer les commandes suivantes pour installer les dépendances:
$ pacman -Su
$ pacman -S --needed base-devel mingw-w64-x86_64-toolchain
(defaut=all)
$ pacman -S gitCet environnement de travail est nécessaire pour installer ensuite nos outils de simulations.
GHDL
GHDL est le simulateur libre de base pour le VHDL. Nous l’installerons avec la commande suivante tirée du tutoriel de darkmagicdesign.
$ pacman -S mingw-w64-x86_64-ghdl-llvmYosys
Yosys est inclue comme package pacman, ce qui nous simplifie grandement la vie :
$ pacman -S mingw-w64-x86_64-yosysGTKwave
$ pacman -S mingw-w64-x86_64-gtkwaveghdl-yosys-plugin
Le package «eda» fait doublon avec certain paquet installé avant, mais en lançant la commande suivante :
$ pacman -S mingw-w64-x86_64-edaOn est sûr d’avoir Yosys compilé en statique avec l’extension GHDL.
python3
$ pacman -S mingw-w64-x86_64-python-scipy mingw-w64-x86_64-python-matplotlib mingw-w64-x86_64-python-numpy
$ pacman -S --needed make mingw-w64-x86_64-gcc mingw-w64-x86_64-python3-pip mingw-w64-x86_64-python3-setuptools mingw-w64-x86_64-python3-wheelÀ ce point de l’installation on peut fermer la fenêtre de console pour aller ouvrir la console nommée «MSYS2 MINGW64» dans laquelle on exécutera les programmes fraîchement installés.
Le répertoire «home/user» de cette console se retrouve ensuite dans le répertoire C:\msys2\home de votre ordinateur.
Cocotb
Cocotb utilise l’installateur de python nommé «pip»:
$ pip install --no-build-isolation cocotb
$ pip install --no-build-isolation pytest
$ pip install --no-build-isolation cocotbext-axiPour finir
En ouvrant la console nommée «MSYS2 MINGW64» on est sûr d’avoir désormais un environnement de simulation correct pour développer des IP sous Windows.
L’exécution de ses différents makefile habituels est presque transparente. Il faudra quand même adapter certaine ligne de commande. Par exemple avec GHDL il est obligatoire d’élaborer le design avec «-e» avant de le lancer avec «-r». Alors que sous Linux on peut passer directement de l’analyse à l’exécution, GHDL devine ce qu’il faut élaborer.
ClaSH un HDL basé sur Haskell
La version 1.0 de CλaSH est sortie en septembre 2019. Profitons de cette sortie pour présenter ce langage de description matériel basé sur Haskell.

Mais qu’est-ce que CλaSH ? On pourrait commencer par le définir en décrivant ce qu’il n’est pas :
- CλaSH (of cλaN ?) n’est pas un jeu vidéo se jouant en caressant un téléphone.
- CλaSH n’est pas un groupe de musique se demandant s’il doit rester ou partir.
- CλaSH n’est pas un HLS (High Level Synthesis). La fonction d’un logiciel HLS consiste à convertir un algorithme écrit dans un langage de programmation classique (très souvent du C) dans une architecture numérique en Verilog/VHDL.
Non.
CλaSH est un langage de description matériel basé sur le langage fonctionnel Haskell.
Le langage Haskell est né dans les années 90, fondé par une société secrète de mathématiciens qui voulait reprendre le contrôle des ordinateurs. En effet, vexés de voir tous ces geeks maîtriser cette machine mieux qu’eux ils décidèrent de se réunir de manière anonyme dans une cave (où il fallait entrer avec un mot de passe à base de développement limités sur un Algèbre commutatif isomorphe) pour fonder un nouveau langage compris par eux seuls. Le Haskell était né ! Enfin je crois 😉
Haskell est un langage fonctionnel, qui nous impose une autre façons de penser un programme informatique. Du dire des auteurs de CλaSH, le paradigme fonctionnel est plus à même de décrire du matériel que le paradigme impératif.
Un composant décrit en CλaSH est directement convertible en Verilog ou en VHDL (les deux sont gérés dans la version 1.0). Ce qui fait qu’un composant décrit en CλaSH est synthétisable avec n’importe quel logiciel de synthèse FPGA.
Dans le cas de ce type de langage on parle de générateur de code, un peu comme Chisel (basé sur Scala), Migen/Litex (basé sur Python) ou SpinalHDL (basé également sur Scala). Ces langages sont en fait des librairies ou des modules du langage auquel ils sont accolés.
Cette modularité permet de profiter d’un langage souvent bien établi avec énormément de fonctions optimisées (Scala, Python, Haskell…).
Le paradigme fonctionnel n’est pas du tout quelque chose qui coule de source pour un simple électronicien comme votre serviteur. Cette dépêche a donc été un peu différée le temps d’avaler les 100 premières pages de tutoriel permettant de faire un simple « hello world » en Haskell. Puis d’avaler le tutoriel CλaSH pour enfin faire clignoter cette fameuse LED sur un kit FPGA low cost de base.
Nous allons donc tenter un petit CλaSHtest permettant de faire clignoter une led.
Le type de base manipulé en CλaSH est le Signal. CλaSH ne permettant que des descriptions synchrones, un Signal représente une liste infinie de valeurs synchronisée sur une horloge et un reset pour la valeur initiale. L’horloge et le reset du signal sont décrit par le Domaine dom du signal. La forme d’un Signal est donc la suivante :
Signal (dom :: Domain) a
En logique synchrone, le composant de base est le registre, nommé register:
register
( HiddenClockResetEnable dom dom
, NFDataX a )
=> a
-> Signal dom a
-> Signal dom a
Son fonctionnement est assez basique : La valeur initiale (de reset) est donnée en premier argument, le second argument est le signal d’entrée qui est recopié sur le signal de sortie (valeur de retour de la fonction). On peut utiliser CλaSH en ligne de commande avec la commande clash.clashi.
$ clash.clashi
Clashi, version 1.0.1 (using clash-lib, version 1.0.1):
http://www.clash-lang.org/ :? for help
Clash.Prelude>
Mais on préférera rapidement enregistrer notre module dans un fichiers source au format *.hs.
Pour faire clignoter une LED dans un FPGA, la première chose à mettre en place est un compteur :
Clash.Prelude> counter = register 0 counter + 1
Cette fonction counter que nous venons de créer retourne un registre initialisé à 0 et qui ajoute 1 à sa sortie à chaque coup d’horloge. La définition est récursive, c’est à dire qu’elle ajoute 1 à elle même. Et comme on commence à 0 et qu’on ajoute 1, la valeur initiale sera 1.
Cette fonction étant infinie, si nous voulons connaitre des valeurs il faut échantillonner :
Clash.Prelude> sampleN @System 10 counter
[1,1,2,3,4,5,6,7,8,9]
On constate que la première valeur est en double car c’est la valeur initiale, avant le premier coup d’horloge. @System désigne le domaine d’horloge/reset/enable utilisé. @System est le domaine général, nous pourrions appliquer un domaine (dom) spécifique à une architecture comme @XilinxSystem ou @IntelSystem.
Le problème avec ce compteur c’est qu’il incrémente à l’infini, nous on voudrait un compteur avec une limite et qui se remet à 0 à une certaine valeur comme ça :
Clash.Prelude> counter value = if(value < 100) then value + 1 else 0
Clash.Prelude> counter 10
11
Clash.Prelude> counter 0
1
Clash.Prelude> counter 101
0
[notes]
Je ne sais pas si je vais réussir à comprendre l’exemple de led qui clignote donné sur le blog de l’auteur de clash en fait.
Je suis parti un peu la fleur au fusil pour faire cette dépêche, mais je me rend compte que l’apprentissage de Clash (et surtout Haskell) est un loooong chemin.
Bref, je crois que je ne vais pas réussir à finir cette dépêche. Peut-être un jour aurais-je suffisamment de bouteille en Haskell pour comprendre Clash, mais là …
Simulons la FFT de Xilinx
Après avoir simulé des FFT avec Python et pylab, voyons comment les intégrer dans un FPGA réel de Xilinx.
Faire une FFT dans un FPGA est quelque chose qui n’est pas trivial. L’avantage, suivant la taille du FPGA, est de pouvoir en faire tourner plusieurs en parallèle pour accélérer le traitement. L’inconvénient étant le temps de développement qui est décuplé par rapport à une solution embarquée sur les habituels DSP ou microcontrôleurs.
Pour accélérer le développement, l’utilisation de modules fournis par les constructeurs est très tentante. Bien sûr, si on utilise la FFT d’un constructeur X, elle ne sera pas utilisable sur le FPGA du constructeur Y… Mais c’est de bonne guerre.
Plus gênant est la difficulté de simuler le module sur son PC pour valider l’algorithme que l’on souhaite mettre en œuvre.
C’est pour cela que Xilinx fournit un modèle C de sa FFT. Modèle que l’on peut utiliser gratuitement avec GCC.
Voyons voir comment mettre tout ça en œuvre.
Installation du modèle
Pour compiler le modèle il faut d’abord le générer à partir d’un projet Vivado. On crée donc un projet Vivado avec un FPGA cible et on instancie le bloc «Fast Fourrier Transform» dans l’«IP designer». Pour pouvoir générer le modèle il faut que les entrées/sorties soient connectées à quelques chose, dans notre cas nous nous contenterons d’exporter les ports.
L’archive au format zip est générée dans le répertoire suivant :
test_fft/test_fft.gen/sources_1/bd/fft_test_design/ip/fft_test_design_xfft_0_0/cmodel/xfft_v9_1_bitacc_cmodel_lin64.zipArchive que l’on dézippera dans le répertoire de son choix :
$ unzip xfft_v9_1_bitacc_cmodel_lin64.zip
$ ls -l
gmp.h
libgmp.so.11
libIp_xfft_v9_1_bitacc_cmodel.so
make_xfft_v9_1_mex.m
run_bitacc_cmodel.c
run_xfft_v9_1_mex.m
xfft_v9_1_bitacc_cmodel.h
xfft_v9_1_bitacc_mex.cppet à laquelle nous ajouterons un fichier main() et un Makefile. Par contre ne rêvez pas, il n’y a pas les sources du modèle 😉 le modèle se trouve dans le fichier binaire de librairie libIp_xfft_v9_1_bitacc_cmodel.so
L’explication pour la compilation est donnée sur le site officiel. Avec g++ ça donne :
$ g++ -std=c++11 -I. -L. -lgmp -Wl,-rpath,. run_bitacc_cmodel.c -o run_fft -lIp_xfft_v9_1_bitacc_cmodelLa compilation génère un binaire nommé run_fft qu’il faut lancer en intégrant les librairies du répertoire courant pour le lien dynamique :
$ LD_LIBRARY_PATH=$$LD_LIBRARY_PATH:. ./run_fft
Running the C model...
Simulation completed successfully
Outputs from simulation are correct
$ Le résultat est relativement frustrant: certes il n’y a pas d’erreur, mais enfin bon … on n’est pas super avancé. On aimerait bien avoir de belles courbes et pouvoir admirer le résultat spectral de cette FFT !
Pour cela il va falloir se plonger dans le code «main()» et injecter son propre signal.
Plongée dans le code
Pour avoir la documentation du modèle on pourra bien sûr se référer à la documentation officiel, mais on peut également se plonger dans le header xfft_v9_1_bitacc_cmodel.h qui est bien commenté.
Le calcul est lancé avec la fonction xilinx_ip_xfft_v9_1_bitacc_simulate déclarée ainsi :
/**
* Simulate this bit-accurate C-Model.
*
* @param state Internal state of this C-Model. State
* may span multiple simulations.
* @param inputs Inputs to this C-Model.
* @param outputs Outputs from this C-Model.
*
* @returns Exit code Zero for SUCCESS, Non-zero otherwise.
*/
Ip_xilinx_ip_xfft_v9_1_DLL
int xilinx_ip_xfft_v9_1_bitacc_simulate
(
struct xilinx_ip_xfft_v9_1_state* state,
struct xilinx_ip_xfft_v9_1_inputs inputs,
struct xilinx_ip_xfft_v9_1_outputs* outputs
);L’état est créé avec la fonction xilinx_ip_xfft_v9_1_create_state() et la structure d’entrée (inputs) possède un tableau de double pour la partie imaginaire et un tableau de double pour la partie réelle. La taille de la FFT étant donnée en 2^n par l’attribut nfft.
struct xilinx_ip_xfft_v9_1_inputs
{
int nfft; //@- log2(point size)
double* xn_re; //@- Input data (real)
int xn_re_size;
double* xn_im; //@- Input data (imaginary)
int xn_im_size;
int* scaling_sch; //@- Scaling schedule
int scaling_sch_size;
int direction; //@- Transform direction
}; // end xilinx_ip_xfft_v9_1_inputsLa structure de sortie est encore plus simple :
struct xilinx_ip_xfft_v9_1_outputs
{
double* xk_re; //@- Output data (real)
int xk_re_size;
double* xk_im; //@- Output data (imaginary)
int xk_im_size;
int blk_exp; //@- Block exponent
int overflow; //@- Overflow occurred
}; // xilinx_ip_xfft_v9_1_outputsDans l’exemple donnée, la partie imaginaire est fixée à 0 sur les 1024 échantillons et la partie réel à 0.5.
// Create input data frame: constant data
double constant_input = 0.5;
int i;
for (i=0; i<samples; i++) {
xn_re[i] = constant_input;
xn_im[i] = 0.0;
}Si le signal est constant, en toute logique seule la fréquence continue (0Hz) doit être différente de 0. C’est ce qui est vérifié après avoir effectué le calcul :
// Check xk_re data: only xk_re[0] should be non-zero
double expected_xk_re_0;
if (C_HAS_SCALING == 0) {
expected_xk_re_0 = constant_input * (1 << C_NFFT_MAX);
} else {
expected_xk_re_0 = constant_input;
}
if (xk_re[0] != expected_xk_re_0) {
cerr << "ERROR:" << channel_text << " xk_re[0] is incorrect: expected " << expected_xk_re_0 << ", actual " << xk_re[0] << endl;
ok = false;
}
for (i=1; i<samples; i++) {
if (xk_re[i] != 0.0) {
cerr << "ERROR:" << channel_text << " xk_re[" << i << "] is incorrect: expected " << 0.0 << ", actual " << xk_re[i] << endl;
ok = false;
}
}
// Check xk_im data: all values should be zero
for (i=1; i<samples; i++) {
if (xk_im[i] != 0.0) {
cerr << "ERROR:" << channel_text << " xk_im[" << i << "] is incorrect: expected " << 0.0 << ", actual " << xk_im[i] << endl;
ok = false;
}
}Transformée de wavelet
Tout ceci n’est pas très parlant pour le moment, testons maintenant le modèle sur la «wavelet» générée à partir d’un script python. Le script permettant de générer le signal et de l’écrire dans un fichier *.txt se trouve dans le répertoire cmodel du dépot github.
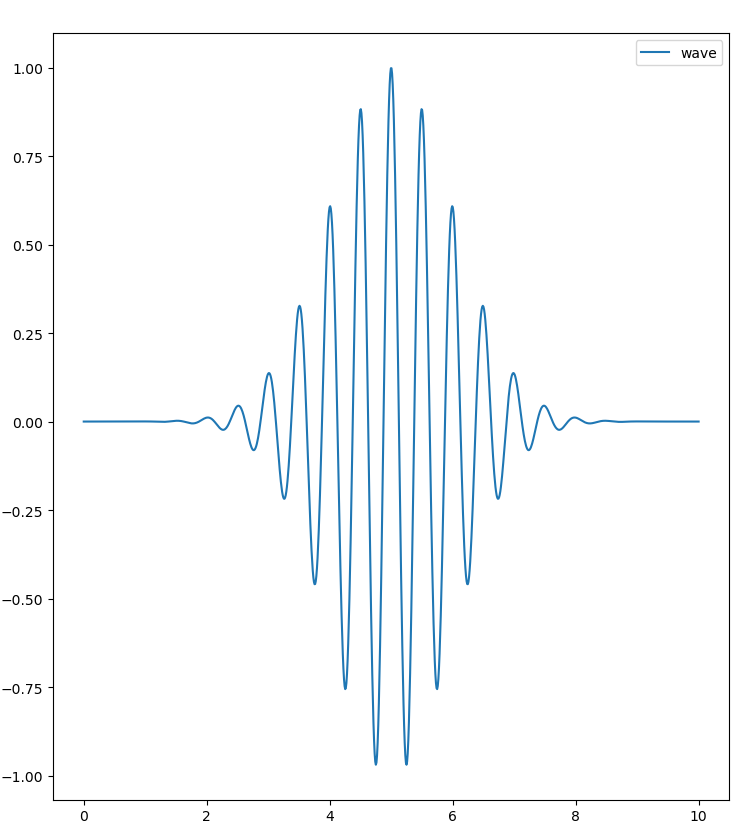
Le script génère un fichier ysig.txt avec toutes les valeurs flottantes écrites en ASCII. On va ensuite relire le fichier avec le programme C++ :
// Read input data from file ysig.txt
std::ifstream yfile; yfile.open("ysig.txt");
if(!yfile.is_open()){
perror("Open error");
exit(EXIT_FAILURE);
}
string line;
int i=0;
while(getline(yfile, line)){
xn_re[i] = stof(line);
cout << stof(line) << endl;
xn_im[i] = 0.0;
i++;
}Le programme écrira le résultat sous dans le fichier xfft_out.txt une fois le résultat calculé:
// save outputs in xfft_out.txt
std::ofstream outfile; outfile.open("xfft_out.txt");
if(outputs.xk_re_size != outputs.xk_im_size){
printf("Error imaginary part size is not equal to real part");
}
for(int i=0; i < outputs.xk_re_size; i++){
outfile << outputs.xk_re[i] << ", " << outputs.xk_im[i] << endl;
}
Fichier que l’on relira pour l’afficher au moyen du script python plot_fft.py
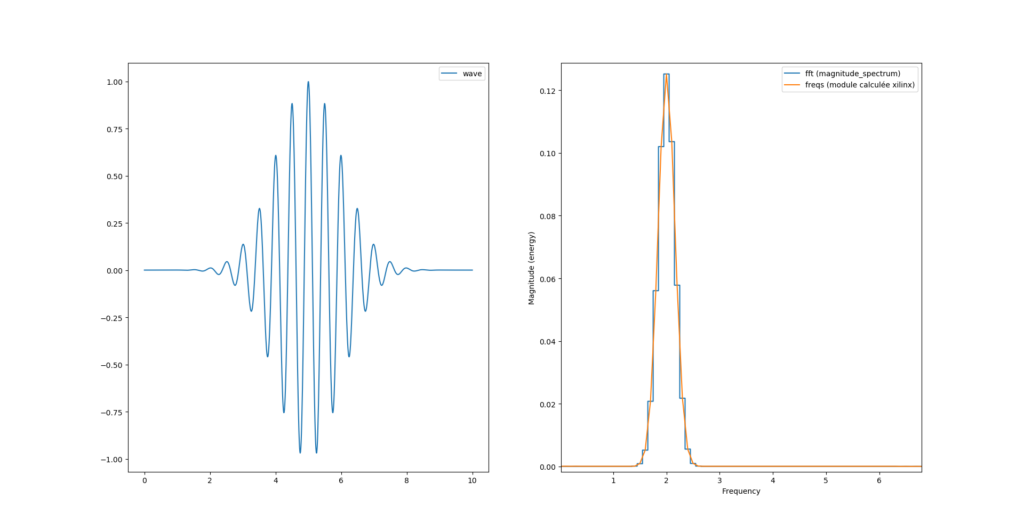
Et nous avons la bonne surprise d’obtenir le même spectre du module qu’avec la fonction de pylab.
On peut maintenant jouer avec les paramètres du module Xilinx et affiner notre modèle de simulation avant de le synthétiser dans un FPGA (de chez Xilinx évidement 😉
Traitement numérique du signal, prise de notes
On dit souvent que pour bien apprendre un sujet en informatique il faut écrire une doc. Pour des besoins pro j’ai du me re-mettre au traitement numérique du signal. Je commence en général par un bouquin et un projet. Pour le projet comme c’est du pro je c’est à ma discrétion, par contre pour le bouquin je me suis plongé dans le livre de Richard G.Lyons «Understanding digital signal processing» qui a le mérite d’être richement illustré de graphes et d’équations avec beaucoup d’explications visuelles et «avec les mains».

L’idée de cette note est donc de faire des exercices en rapport avec ce qui est dans ce livre mais pas que, le tout de manière pratique en python et de voir les implications que ça peut avoir avec les FPGA.
Un signal discret
Dans un premier temps nous aurons besoin de numpy et pylab en python3
import numpy as np
import pylab as pltLe signal de base est une sinusoïde. Pour représenter un signal de 1 Hertz en python on va d’abord créer un tableau d’un certain nombre de valeur de 0 à 1 secondes :
# Freq
f0 = 1
# 40 points de 0 à 39
t = np.linspace(0, 1, 40)Puis calculer le sinus
y = np.sin(2*math.pi*f0*t)Signal qu’il est facile de «plotter» ensuite :
plt.plot(t, y)
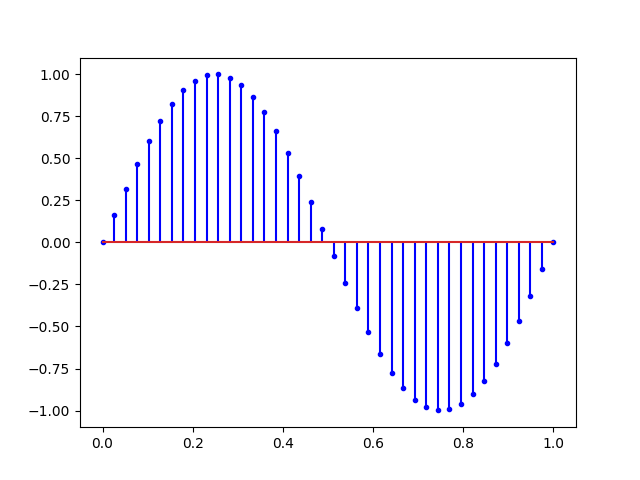
plt.show()Ce qui nous donne cette belle courbe de sinus :
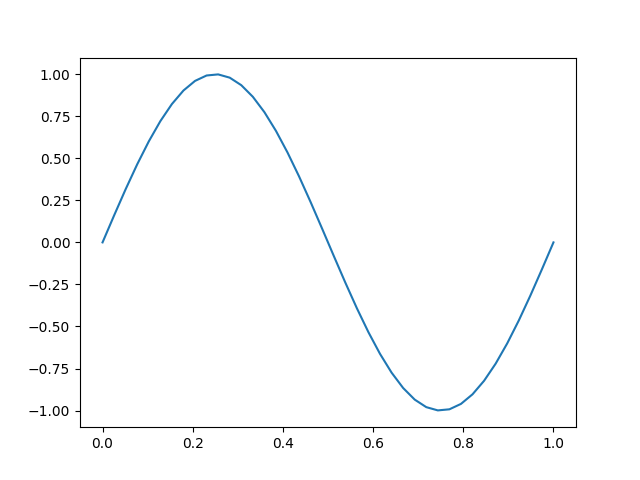
Mais pour bien se représenter un signal numérique il ne faut pas relier les points. Il vaut mieux mettre des points avec des lignes verticales comme ceci :
fix, ax = plt.subplots()
ax.stem(t, y, 'b', markerfmt="b.")
plt.show()Ce qui nous donne la figure suivante :
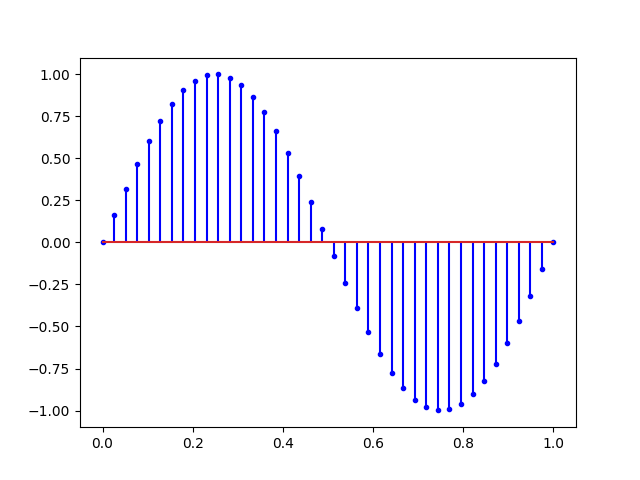
Cette dernière figure illustre bien la notion d’échantillonnage avec une fréquence d’échantillonnage fs de 40Hertz (temps en secondes et 40 points) soit :
# Freq
f0 = 1
# Temps total
T = 1
# Nombre de points:
N = 40
# Fréquence d’échantillonnage :
print(f"fs = {N/T} Hertz")
# fs = 40.0 HertzIci, la fréquence d’échantillonnage (40Hertz) est largement supérieur à la fréquence du signal enregistré (1 Hertz). On peut s’amuser maintenant à monter la fréquence du signal à la fréquence de Nyquist :
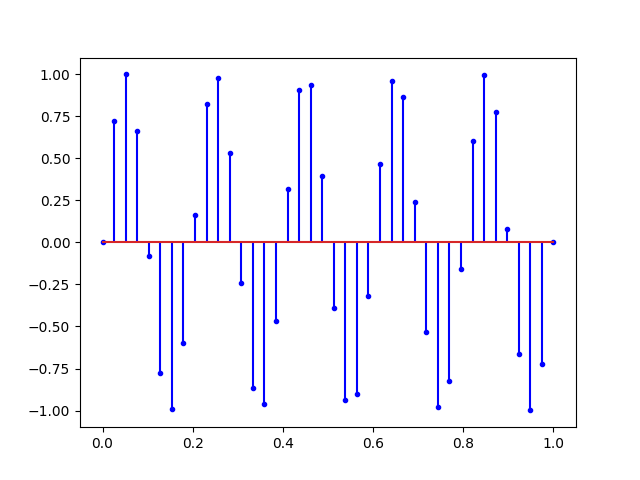
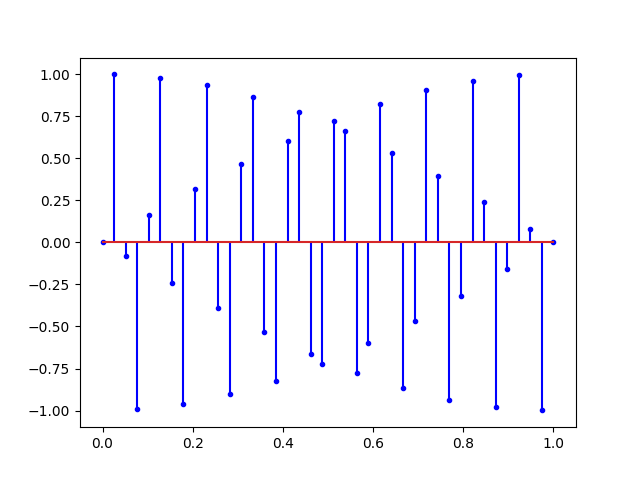
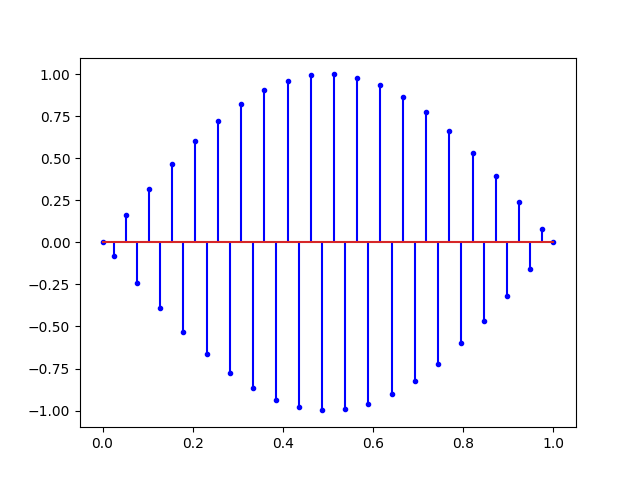
Ce que nous dit Nyquist, c’est qu’avec tous les signaux ci-dessus, il est possible de retrouver la sinusoïde du début. Mais si on augmente encore la fréquence on obtient un repliement du spectre.
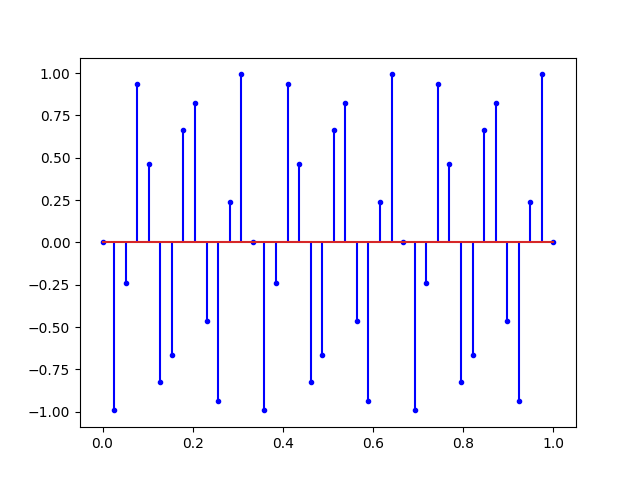
On peut ajouter le l’analyse de spectre en augmentant également le nombre de points mesuré :
# Freq
f0 = 1
# Temps total
T = 1
# Nombre de points:
N = 100
# 100 points de 0 à 99
t = np.linspace(0, T, N)
y = np.sin(2*np.pi*f0*t)
fix, ax = plt.subplots(1,2)
ax[0].stem(t, y, 'b', markerfmt="b.")
ax[1].magnitude_spectrum(y, Fs=N/T, ds="steps-mid")
plt.show()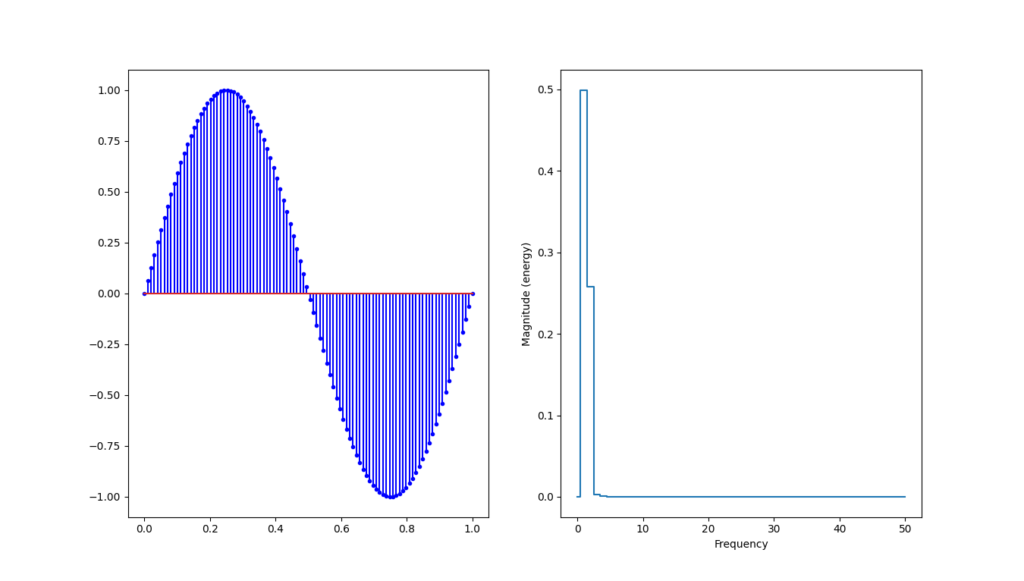
Ondelettes
Pour faire une ondelette (wavelet) on multiplie un cosinus (périodique) avec une gaussienne (exp(-t²/2)) :
# Décalage en seconde:
retard = 5
y = np.cos(2*np.pi*f0*t)*np.exp(-np.power(t-retard,2)/2)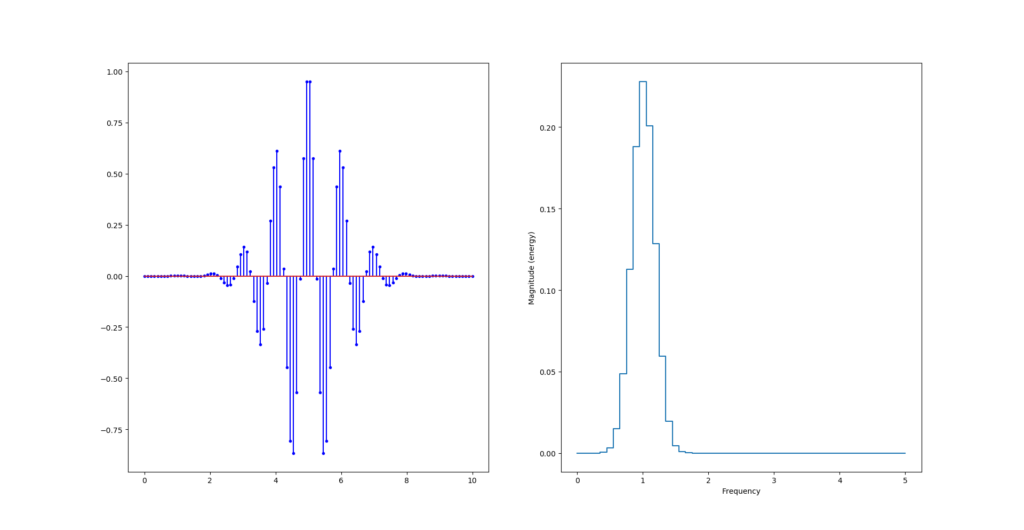
La vidéo suivante explique tout ce que vous avez toujours voulu savoir sur les ondelettes.
Si on change la fréquence du signal, en passant à 2Hz par exemple. On se rend compte que l’échantillonnage tronque les maximum locaux :
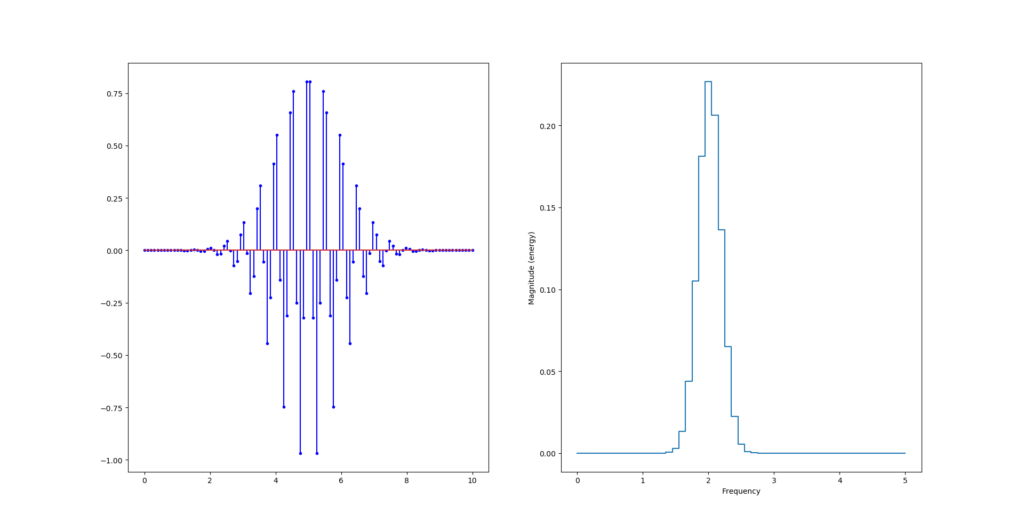
Ce qui casse la symétrie de la courbe.
Hilbert avec scipy
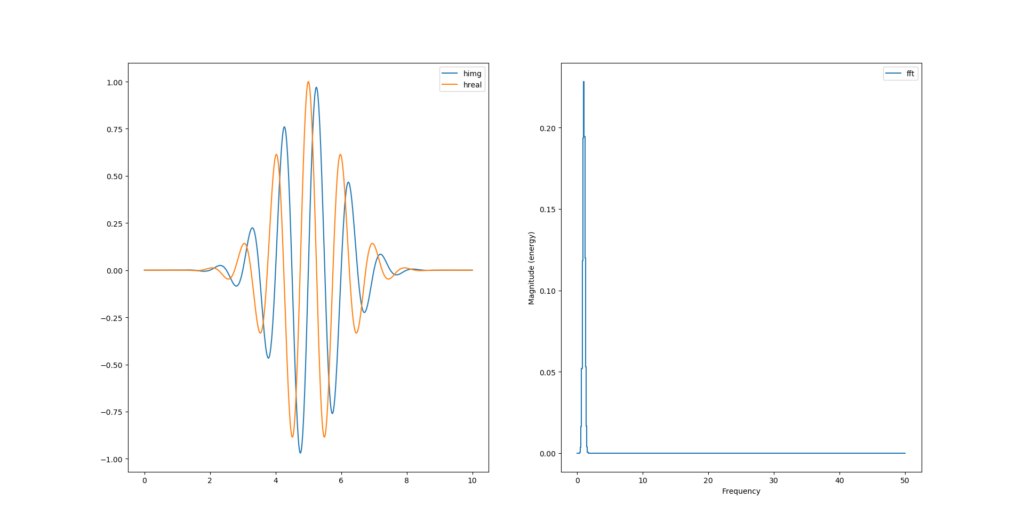
La transformée de hilbert permet de calculer la partie imaginaire du signal réel. Le package python nommé scipy inclue la fonction qui la calcule.
[...]
from scipy import signal
[...]
# morlet wavelet
y = np.cos(2*np.pi*f0*t)*np.exp(-np.power(t-retard,2)/2)
himg = signal.hilbert(y).imag
hreal = signal.hilbert(y).real
[...]
Comme nous avons la partie réelle et la partie imaginaire de notre signal, il est possible désormais de calculer son module pour en tirer l’enveloppe:
# morlet wavelet
y = np.cos(2*np.pi*f0*t)*np.exp(-np.power(t-retard,2)/2)
himg = signal.hilbert(y).imag
hreal = signal.hilbert(y).real
habs = np.sqrt(np.power(himg, 2) + np.power(hreal, 2))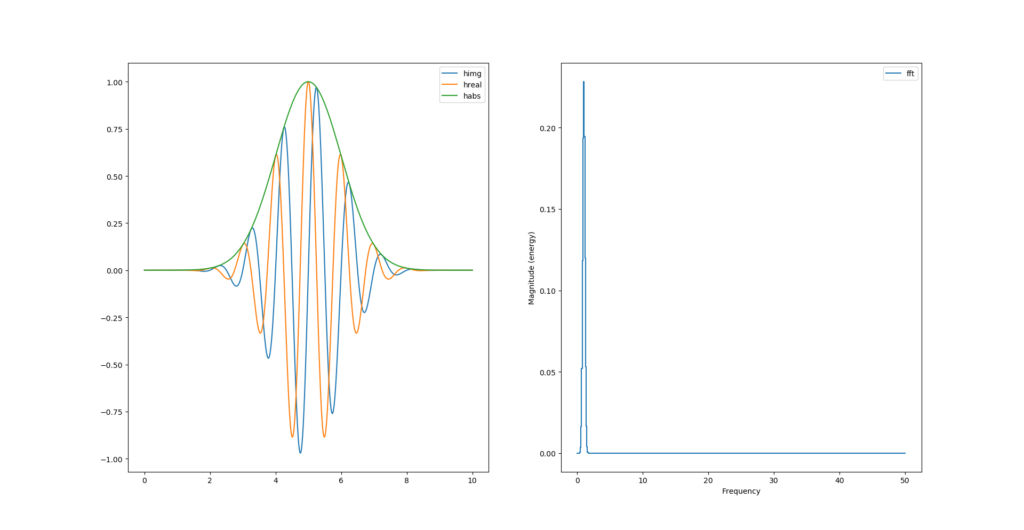
Si l’on diminue la fréquence d’échantillonnage (division par 10) on remarque que l’enveloppe ne passe plus par les maximums. La transformée de Hilbert semble les avoirs tout de même déduit :
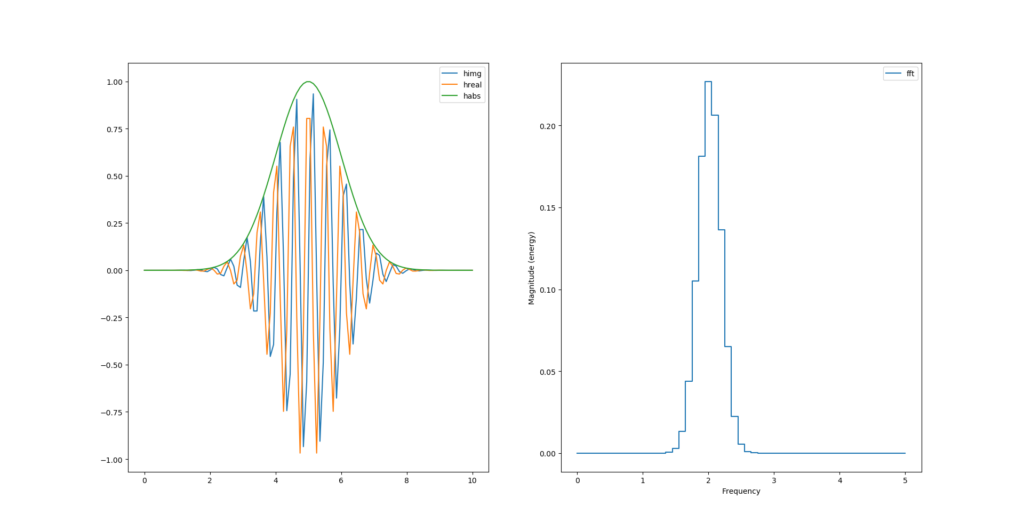
Peut-on calculer l’enveloppe sans racine carré et carré ?
habs = np.abs(himg) + np.abs(hreal)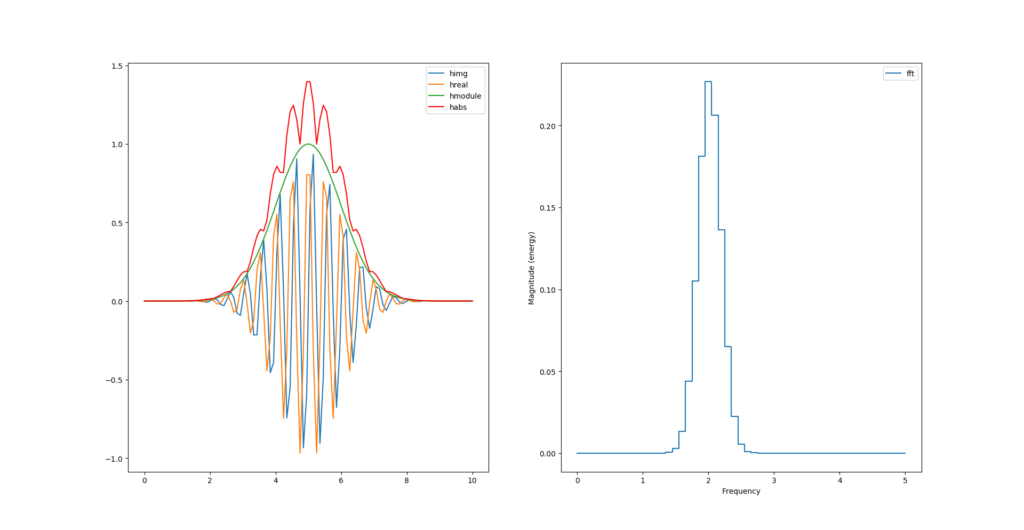
Et juste avec des carrés ?
hsquare= np.power(himg, 2) + np.power(hreal, 2)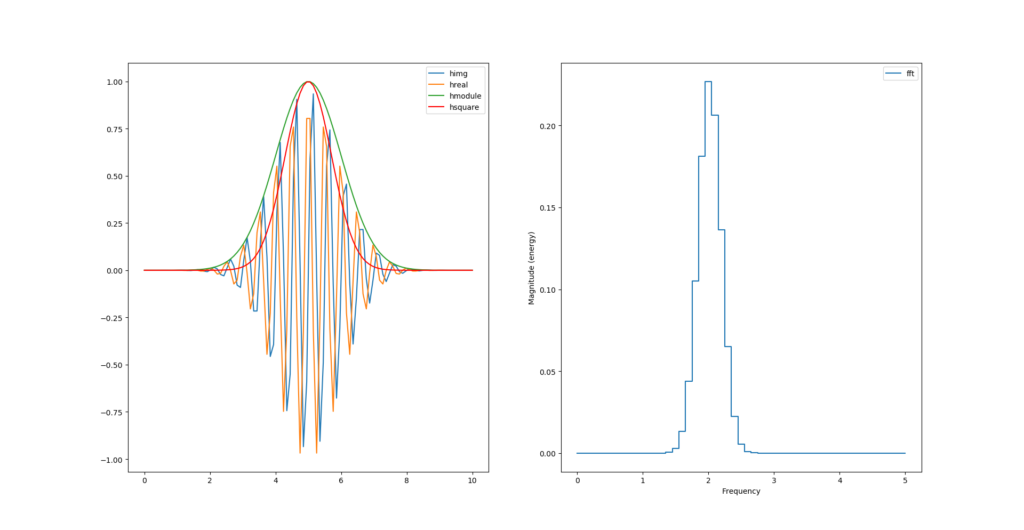
Transformée de Fourrier
Mais que faites vous encore sur ce blog ! Vite allez visionner l’excellente vidéo de 3Blue1Brown qui parle de la transformée de Fourrier avec force de graphes et de dessins. Vous ne verrez plus la transformée de fourrier comme avant 😉
Sinon y a aussi cette formule trouvée sur twitter qui est vraiment très parlante :
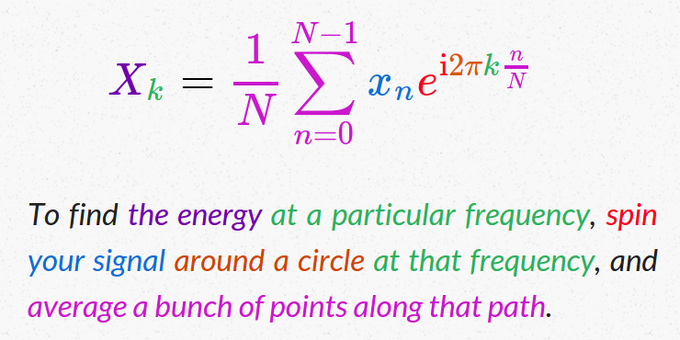
Jusqu’à présent, pour calculer et afficher la transformée de fourrier de notre signal, nous nous sommes servi exclusivement de la fonction magnitude_spectrum() inclue dans pylab. C’est intéressant pour avoir un aperçu du spectre, mais ça ne permet pas de dire que l’on maîtrise ça.
Nombre complexes en python
Python permet visiblement d’utiliser nativement des nombres complexes avec ‘j’ à condition d’y mettre un nombre devant :
In [2]: j
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
<ipython-input-2-3eedd8854d1e> in <module>
----> 1 j
NameError: name 'j' is not defined
In [3]: 1j
Out[3]: 1j
In [4]: 0.02j
Out[4]: 0.02j
In [5]: -3j
Out[5]: (-0-3j)
In [7]: np.exp(1j)
Out[7]: (0.5403023058681398+0.8414709848078965j)
Tentons donc de calculer la transformée de fourrier en mode «brute de force» pour voir:
#temps: 0 points de 0 à N-1
t = np.linspace(0, T, N)
# morlet wavelet
y = np.cos(2*np.pi*f0*t)*np.exp(-np.power(t-retard,2)/2)
# transformée de fourrier
freqs = np.array([])
for k in range(N):
listexp = [y[n]*np.exp(1j*2*np.pi*k*n/N) for n in range(N)]
xk = (1/N)*np.array(listexp).sum()
freqs = np.append(freqs, xk)
#fréquence: 0 points de 0 à N-1
k = np.linspace(0, T, N)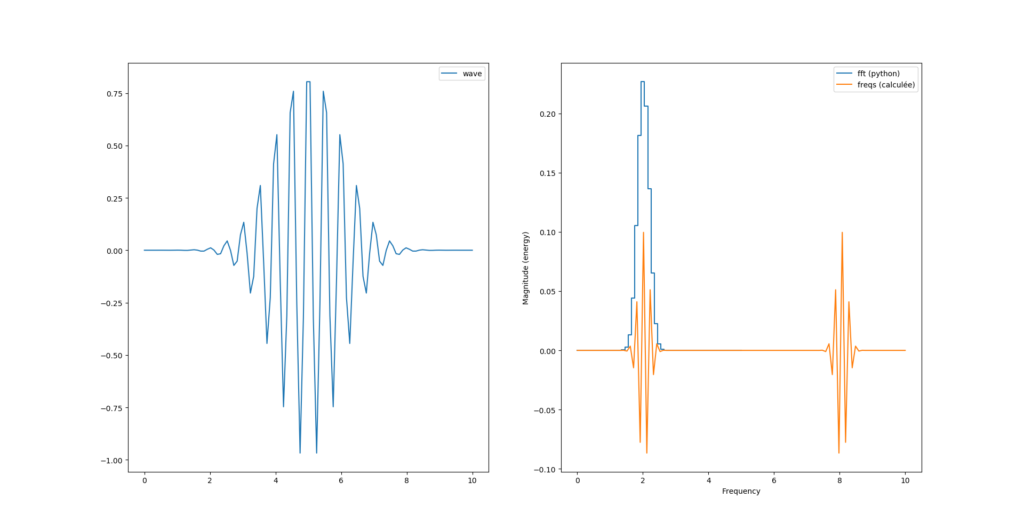
Là ce que nous venons de calculer est la version complexe de la transformée de fourrier dont pylab nous «plot» la partie réelle. Voyons voir le module :
fourrier_module = np.sqrt(np.power(freqs.imag, 2) + np.power(freqs.real, 2))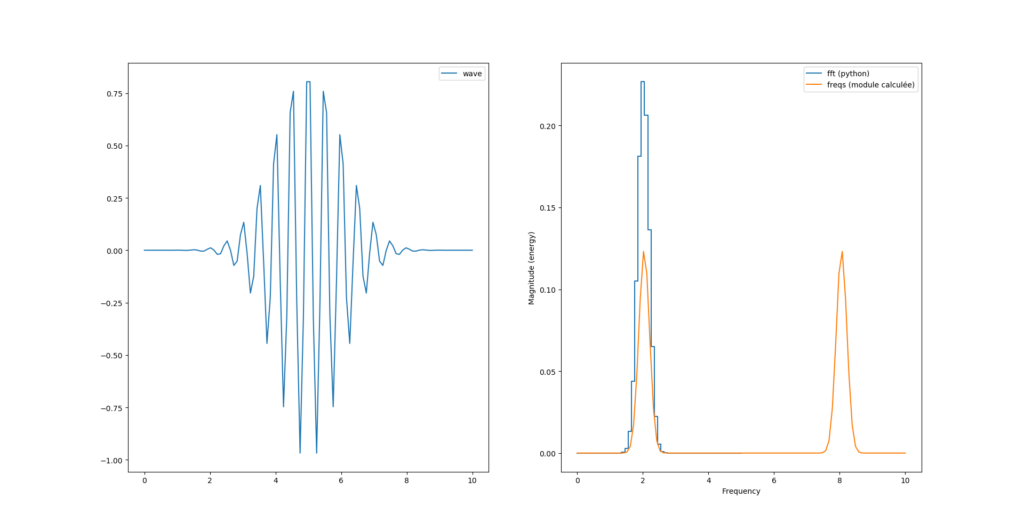
Nous avons donc toujours deux pics, sachant que le second pic est au delà de la fréquence de Nyquist (Fs=10Hz) et semble «normal».
Par contre nous avons un facteur 2 entre le calcul de magnitude de python et celui que l’on vient de calculer.
Peut-être parce que la formule de l’image est celle de la transformée inverse ? La transformée discrète donnée dans le livre est plutôt celle là :
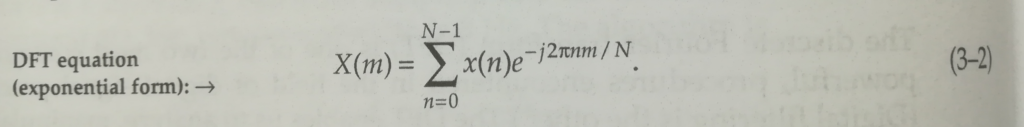
Voyons voir avec cette nouvelle formule :
# transformée de fourrier
freqs = np.array([])
for k in range(N):
listexp = [y[n]*np.exp(-1j*2*np.pi*k*n/N) for n in range(N)]
xk = np.array(listexp).sum()
freqs = np.append(freqs, xk)
fourrier_module = np.sqrt(np.power(freqs.imag, 2) + np.power(freqs.real, 2))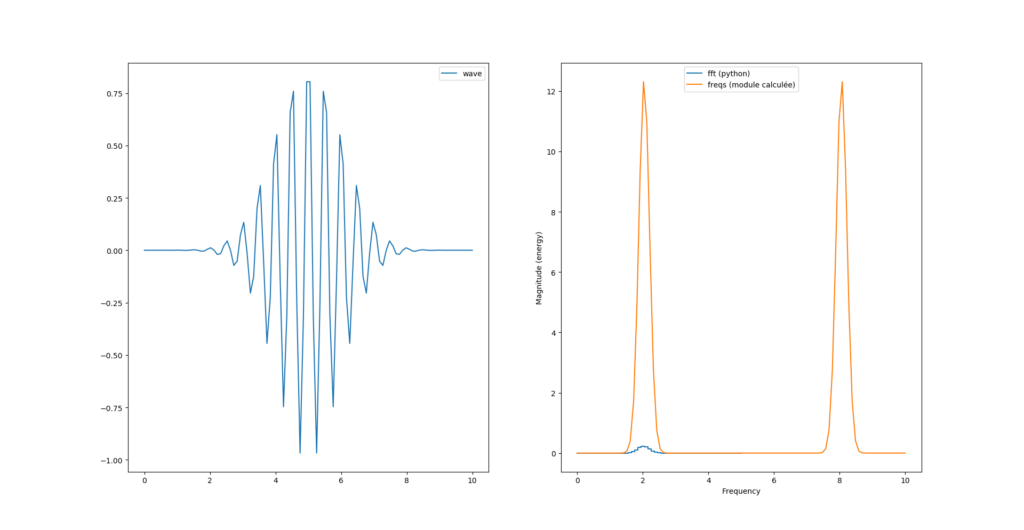
Si on veut «matcher» la courbe de magnitude il faut ajouter un facteur 2/N au calcul du module :
fourrier_module = (2/N)*np.sqrt(np.power(freqs.imag, 2) + np.power(freqs.real, 2))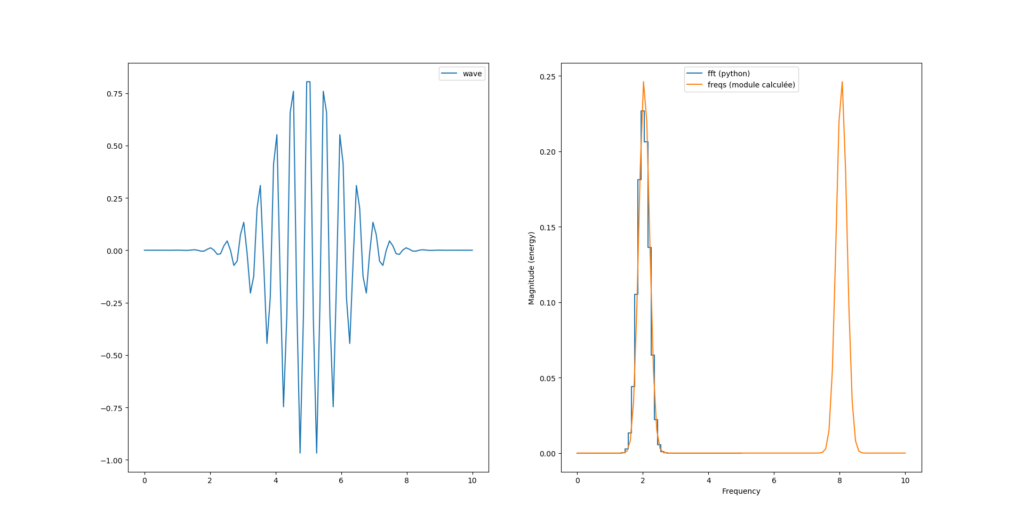
cos – sin
Pour faire entrer le calcul de la transformée dans un FPGA, l’exponentielle d’un complexe n’est pas super pratique. Décomposons donc en différence cos-sin avec la formule d’Euler, on devrait obtenir le même résultat:
# transformée de fourrier
freqs = np.array([])
for k in range(N):
listexp = []
for n in range(N):
angle = 2*np.pi*k*n/N
listexp.append(y[n]*(np.cos(angle) - 1j*np.sin(angle)))
xk = np.array(listexp).sum()
freqs = np.append(freqs, xk)Et nous obtenons exactement le même graphe qu’avant.
C’est sans surprise qu’on obtient la même chose en sommant indépendamment partie réelle et partie imaginaire :
# transformée de fourrier
freqs_real = np.array([])
freqs_img = np.array([])
for k in range(N):
listreal = []
listimg = []
for n in range(N):
angle = 2*np.pi*k*n/N
listreal.append(y[n]*(np.cos(angle)))
listimg.append(y[n]*(-np.sin(angle)))
xkreal = np.array(listreal).sum()
xkimg = np.array(listimg).sum()
freqs_real = np.append(freqs_real, xkreal)
freqs_img = np.append(freqs_img, xkimg)
fourrier_module = (2/N)*np.sqrt(np.power(freqs_img, 2) + np.power(freqs_real, 2))Nous permettant au passage de dégager le ‘j’ des nombres complexes qui ne passe pas très bien dans un FPGA.
Des entiers ou des virgules fixes
Pour le moment c’était facile: on avait les flottant de python. Seulement voilà, dans un FPGA, les flottants ne sont pas simple. Nous avons besoin de fixer la taille (en bits) des variables/registres utilisés. Il faut également fixer la position de la virgule si l’on souhaite simplifier le calcul.
Le second problème nous vient des fonctions sin() et cos() qui ne sont pas calculables simplement. L’astuce consiste à pré-calculer les valeurs et les stocker dans une table qui ira remplir une ROM du FPGA.
Pour gérer des entiers en virgule fixe et de taille hétérogène on installera le module fxpmath :
$ git clone https://github.com/francof2a/fxpmath.git
$ cd fxpmath/
$ python -m pip install -e .Pour commencer on va passer le signal ‘y’ en entier signé sur 16bits avec
# morlet wavelet
y = np.cos(2*np.pi*f0*t)*np.exp(-np.power(t-retard,2)/2)
YTYPE="S1.15"
ysint = Fxp(y, dtype=YTYPE)Le signal se trouvant entre -1 et 1 nous choisirons un format signé sur 16 bits avec tous les chiffres derrière la virgule ‘S1.15’.
Pour les calculs intermédiaires on va rester sur du signé 16 bits mais avec la virgule au milieu cette fois, soit ‘S8.8’:
# transformée de fourrier
freqs_real = np.array([])
freqs_img = np.array([])
for k in range(N):
listreal = []
listimg = []
for n in range(N):
angle = Fxp(2*fixpi*Fxp(k, dtype=DTYPE)*Fxp(n, dtype=DTYPE)/N,
dtype=DTYPE)
listreal.append(Fxp(y[n]*( np.cos(angle)), dtype=DTYPE))
listimg.append (Fxp(y[n]*(-np.sin(angle)), dtype=DTYPE))
xkreal = Fxp(np.array(listreal).sum(), dtype=DTYPE)
xkimg = Fxp(np.array(listimg ).sum(), dtype=DTYPE)
print(f"Freq {k} -> {xkreal}({xkreal.dtype}) + {xkimg}j ({xkimg.dtype})")
freqs_real = np.append(freqs_real, xkreal)
freqs_img = np.append(freqs_img, xkimg)
#fourrier_module = (2/N)*np.sqrt(np.power(freqs_img, 2) + np.power(freqs_real, 2))
fourrier_power = Fxp(Fxp(freqs_img*freqs_img, dtype=DTYPE) + Fxp(freqs_real*freqs_real, dtype=DTYPE), dtype=DTYPE)
fourrier_module = Fxp((2/N)*Fxp(np.sqrt(fourrier_power), dtype=DTYPE), dtype=DTYPE)La première surprise de cette méthode est le temps de calcul: on passe d’un calcul de la transformée quasi instantanée à un calcul qui prend presque une minute.
La seconde surprise vient avec le «bruit haute fréquence» qui apparaît dans le résultat et le second pic qui disparaît.
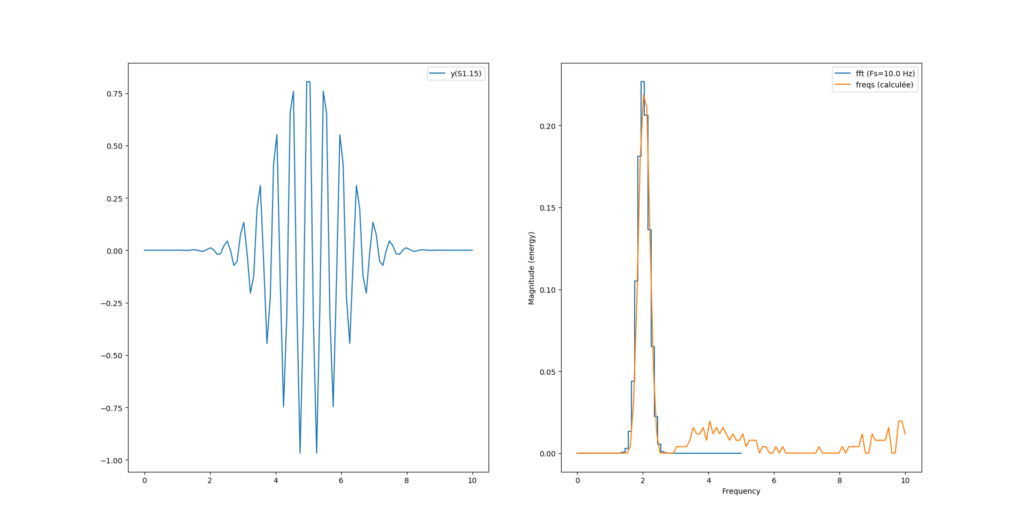
Le problème de ce bruit vient de l’arrondi calculé sur Pi, si on ajuste la virgule de Pi comme ceci :
# Frequence du signal
Sf0 = 2
f0 = (Sf0 * Fs)/T
# Décalage en seconde:
retard = 5
#temps: 0 points de 0 à N-1
t = np.linspace(0, T, N)
# morlet wavelet
y = np.cos(2*np.pi*f0*t)*np.exp(-np.power(t-retard,2)/2)
YTYPE="S1.15"
ysint = Fxp(y, dtype=YTYPE)
DTYPE="S8.8"
D2TYPE="S16.16"
fixpi = Fxp(np.pi, dtype="U3.13")
# transformée de fourrier
freqs_real = np.array([])
freqs_img = np.array([])
for k in range(N):
listreal = []
listimg = []
for n in range(N):
angle = Fxp(2*fixpi*Fxp(k*n, dtype="U16.0")/N, dtype=D2TYPE)
listreal.append(Fxp(y[n], dtype=YTYPE)*Fxp( np.cos(angle), dtype=YTYPE))
listimg.append (Fxp(y[n], dtype=YTYPE)*Fxp(-np.sin(angle), dtype=YTYPE))
xkreal = Fxp(np.array(listreal).sum(), dtype=DTYPE)
xkimg = Fxp(np.array(listimg ).sum(), dtype=DTYPE)
print(f"Freq {k}/{Fs} ({k*T/N}) -> {np.sqrt(xkreal*xkreal + xkimg*xkimg)})")
freqs_real = np.append(freqs_real, xkreal)
freqs_img = np.append(freqs_img, xkimg)
fourrier_power = Fxp(Fxp(freqs_img*freqs_img, dtype=DTYPE) + Fxp(freqs_real*freqs_real, dtype=DTYPE), dtype=DTYPE)
fourrier_module = Fxp((2/N)*Fxp(np.sqrt(fourrier_power), dtype=DTYPE), dtype=DTYPE)
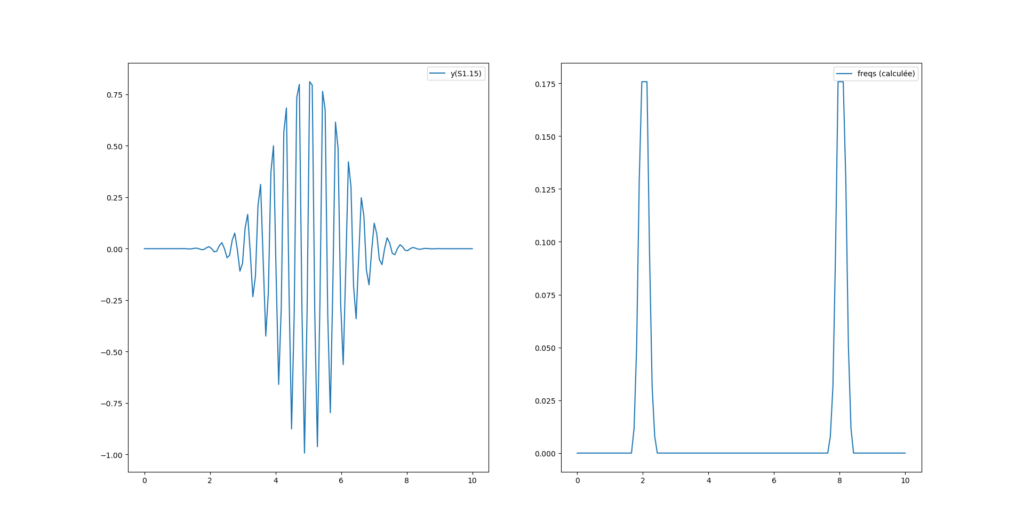
Par contre on a un décalage de fréquence avec la fonction magnitude_spectrum() de pylab :
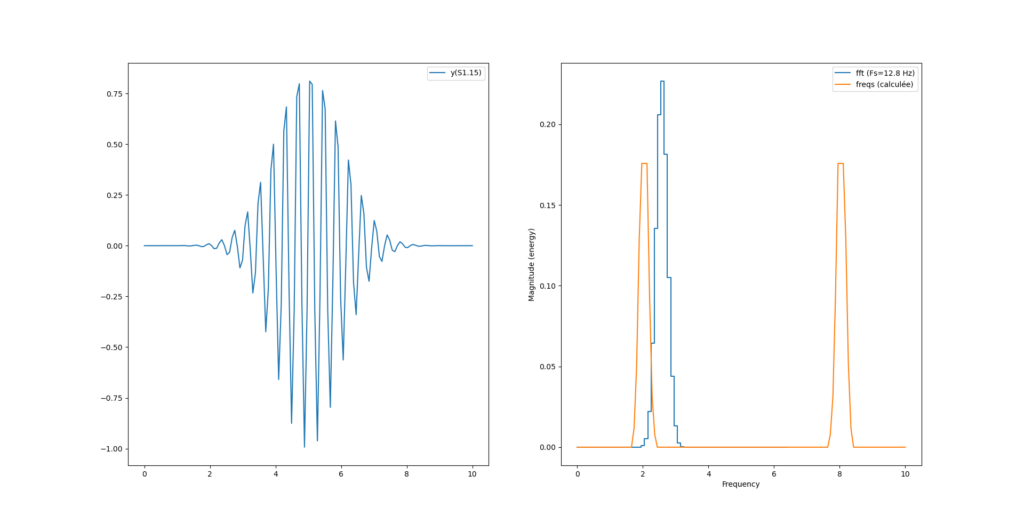
Ce décalage provient de l’axe des x qui n’est pas le même pour le calcul de python et le calcul maison. En effet, notre calcul «à la main» s’étend sur tout l’espace «de nyquist» (0 à N-1) alors que la fonction magnitude_spectrum() n’affiche le spectre que sur la moitée.
Pour recentrer tout ça on peut simplement récupérer la table des fréquences fournie par magnitude_spectrum() et l’utiliser comme axe des x dans l’affichage de notre spectre :
#...
magnitude, freqs, _ = ax[1].magnitude_spectrum(y, Fs=N/T, ds="steps-mid", label=f"fft (Fs={Fs} Hz)")
#...
ax[1].plot(freqs, fourrier_module[:len(freqs)], label = "freqs (calculée)")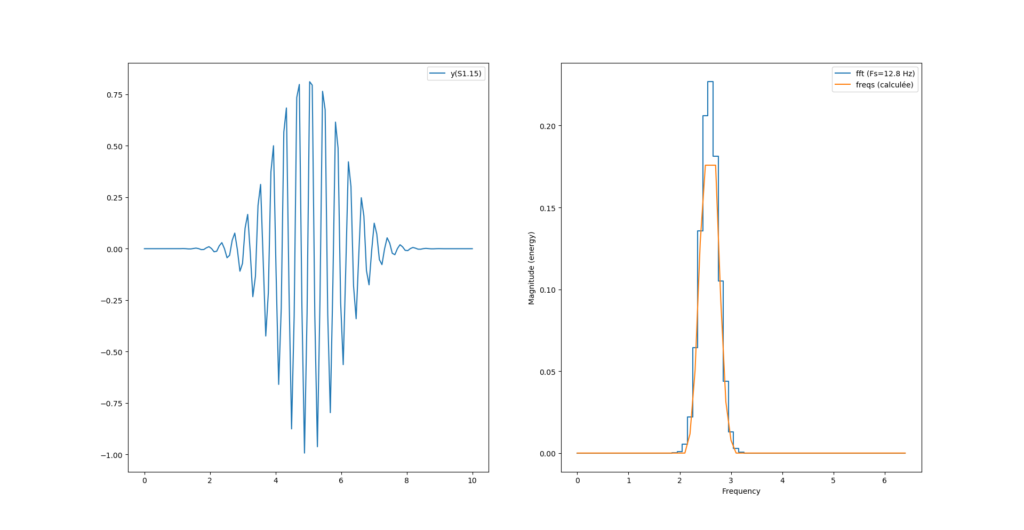
Et nous obtenons la bonne fréquence pour les deux modes de calculs. Reste maintenant un problème de magnitude maximum, est-ce un problème d’arrondi de la virgule fixe ? Possible.
Ressources
Le code de cet article se trouve sur le dépôt github suivant.
RapidSilicon va-t-elle renverser la table ?
Le FLF a été fondé a une époque obscure où il n’existait (quasiment) pas de solution open-source pour travailler sur des FPGA. Seul un petit village d’irréductibles simulateurs comme icarus, ghdl ou verilator maintenaient un semblant de liberté dans cet océan de sombre verrouillage. Il y avait bien VTR et Alliance, mais ils restaient très universitaire et un peu trop centré sur les ASIC.
Puis est arrivé Yosys le logiciel libre de synthèse Verilog accompagné du reverse engineering de l’ICE40 avec Icestorm. Ont suivis Apicula pour les Gowin, X-Ray pour les Xilinx série 7 ou Trellis pour les ECP5 (Voir le tableau des projets de reverse sur le FLF).
Et pour boucler la boucle de développement, le logiciel libre de placement routage nextpnr a émergé ainsi que le logiciel de configuration universelle openFPGALoader.
Toutes ces initiatives ont énormément gagnées en qualité et en crédibilité depuis 3 ou 4 ans et sont en passe de devenir les références dans le monde du FPGA.
À ces nouvelles très réjouissantes se sont ajouté les annonces de plusieurs mise en production de FPGA avec les outils open-source supportés officiellement par les constructeurs. On pense notamment à :
- Quicklogic et son microcontrôleur EOS S3 basé sur un cœur Cortex-M4 couplé à une «zone» de FPGA utilisable intégralement avec des logiciels open source.
- CLEAR: un projet plus anecdotique consistant à générer un FPGA à partir de l’outil open source openFpga et à l’intégrer à la Caravel de la société eFabless pour la graver en 130nm. Pour le coup les outils pour développer le FPGA sont opensource ainsi que les outils pour développer sur le fpga.
- CologneChip et son GateMate: un FPGA à l’architecture assez original notamment pour la partie calcul/dsp mais qui se défend assez bien niveau taille.
Avec toutes ces nouvelles on aurait pensé que cela allait se calmer et que l’on aurait le temps de digérer et faire clignoter quelques LED avant de passer à une vitesse encore supérieure.
ERREUR !
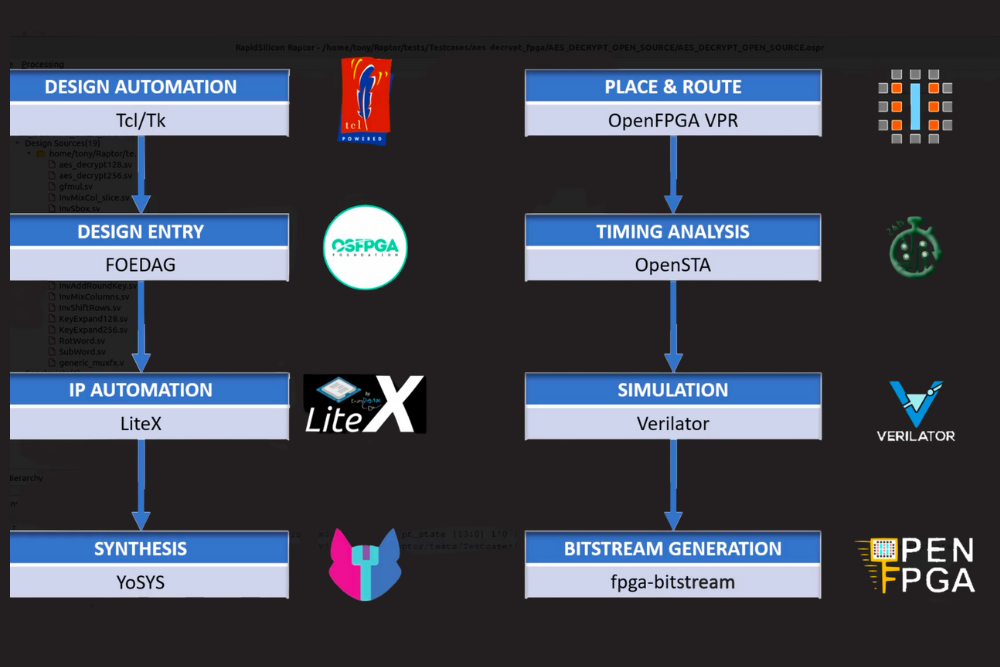
C’était sans compter sur cette société créé en 2020 (et oui toute neuve) et son annonce de sortie du projet Gemini (un poil prétentieux tout de même pour le nom 😉 de faire un SoC haute performances en se basant sur des outils open sources, et oui même pour la fabrication du FPGA. En parallèle du développement silicium, RapidSilicon développe un IDE open source nommé Raptor se basant sur tout un tas de logiciels libres cité au début de cet article :
Un premier échantillonnage de composants en 16nm est déjà sorti des fonderies de TSMC et nous rassure sur la réalité du produit. Nous ne sommes pas dans le cas d’une société qui fait des annonces «vaporware» juste pour faire des levées de fond.

L’architecture du prototype est donnée dans la figure suivante:
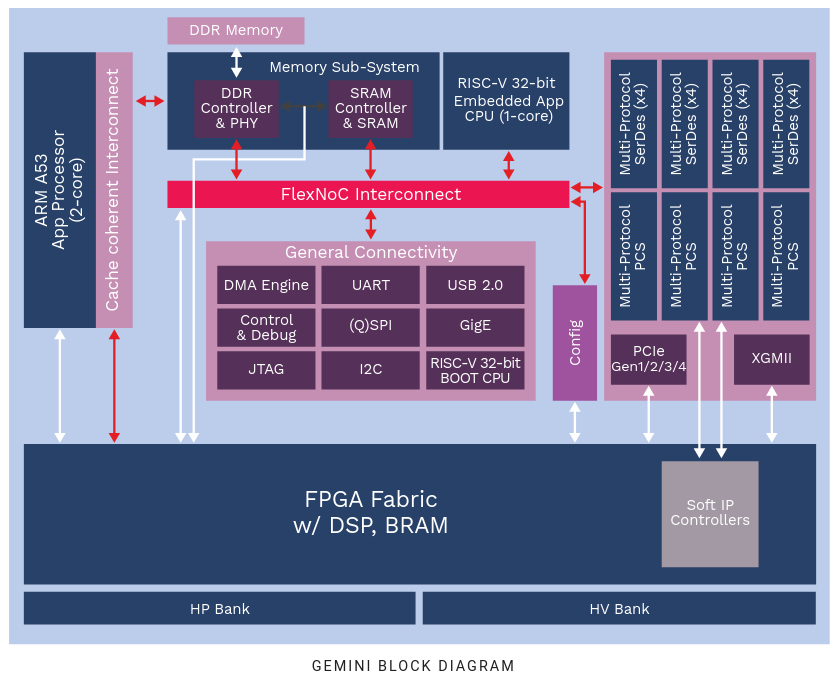
On est donc dans le cas d’un gros SoC-FPGA avec les caractéristiques suivantes :
- Arm A53 Dual-Core
- contrôleur de DDR4
- «Petit» core Risc-V 32bit pour le temps réel et la supervision
- Les ports habituels d’un SoC : UART, USB, SPI, I²C, …
- Du PCIe Gen4, XGMII (pour le réseau)
- Des liens serdes (très) rapide jusqu’à 16Gbits/s
- La zone FPGA n’est pas énorme, mais se défend face aux petit Zynq par exemple :
- 50-75K LUT (6 entrées)
- Blocks DSP (combien ?)
- Block de Ram double port 18kb (Combien ?)
Toutes ces parties sont liée ensemble au moyen d’un bloc d’interconnexion nommé FlexNOC.
Alors ?
Xilinx doit-elle trembler avec son Zynq ? et Microsemi avec son PolarFire SoC ?
L’avenir nous le dira, hâte de voir la suite 🙂
