On dit souvent que pour bien apprendre un sujet en informatique il faut écrire une doc. Pour des besoins pro j’ai du me re-mettre au traitement numérique du signal. Je commence en général par un bouquin et un projet. Pour le projet comme c’est du pro je c’est à ma discrétion, par contre pour le bouquin je me suis plongé dans le livre de Richard G.Lyons «Understanding digital signal processing» qui a le mérite d’être richement illustré de graphes et d’équations avec beaucoup d’explications visuelles et «avec les mains».

L’idée de cette note est donc de faire des exercices en rapport avec ce qui est dans ce livre mais pas que, le tout de manière pratique en python et de voir les implications que ça peut avoir avec les FPGA.
Un signal discret
Dans un premier temps nous aurons besoin de numpy et pylab en python3
import numpy as np
import pylab as pltLe signal de base est une sinusoïde. Pour représenter un signal de 1 Hertz en python on va d’abord créer un tableau d’un certain nombre de valeur de 0 à 1 secondes :
# Freq
f0 = 1
# 40 points de 0 à 39
t = np.linspace(0, 1, 40)Puis calculer le sinus
y = np.sin(2*math.pi*f0*t)Signal qu’il est facile de «plotter» ensuite :
plt.plot(t, y)
plt.show()Ce qui nous donne cette belle courbe de sinus :
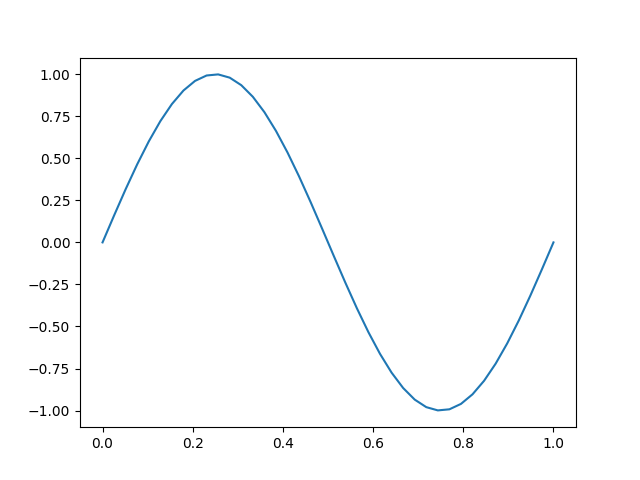
Mais pour bien se représenter un signal numérique il ne faut pas relier les points. Il vaut mieux mettre des points avec des lignes verticales comme ceci :
fix, ax = plt.subplots()
ax.stem(t, y, 'b', markerfmt="b.")
plt.show()Ce qui nous donne la figure suivante :
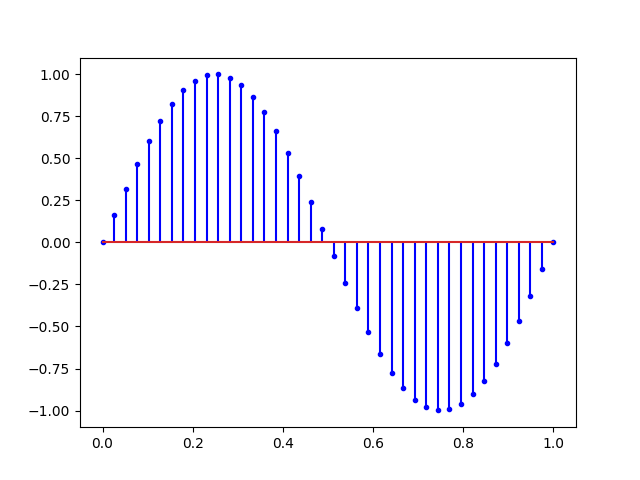
Cette dernière figure illustre bien la notion d’échantillonnage avec une fréquence d’échantillonnage fs de 40Hertz (temps en secondes et 40 points) soit :
# Freq
f0 = 1
# Temps total
T = 1
# Nombre de points:
N = 40
# Fréquence d’échantillonnage :
print(f"fs = {N/T} Hertz")
# fs = 40.0 HertzIci, la fréquence d’échantillonnage (40Hertz) est largement supérieur à la fréquence du signal enregistré (1 Hertz). On peut s’amuser maintenant à monter la fréquence du signal à la fréquence de Nyquist :
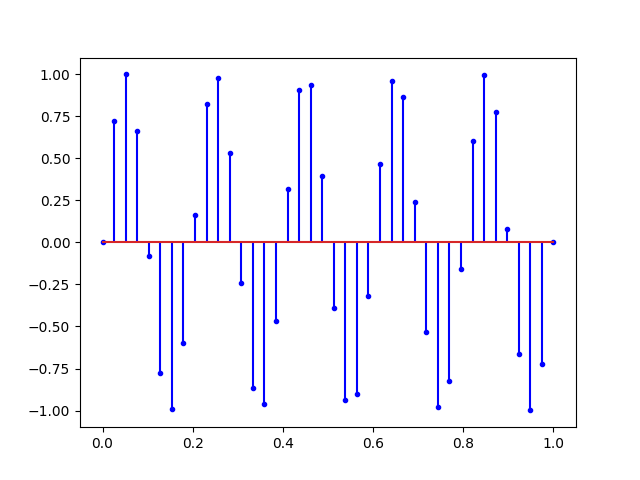
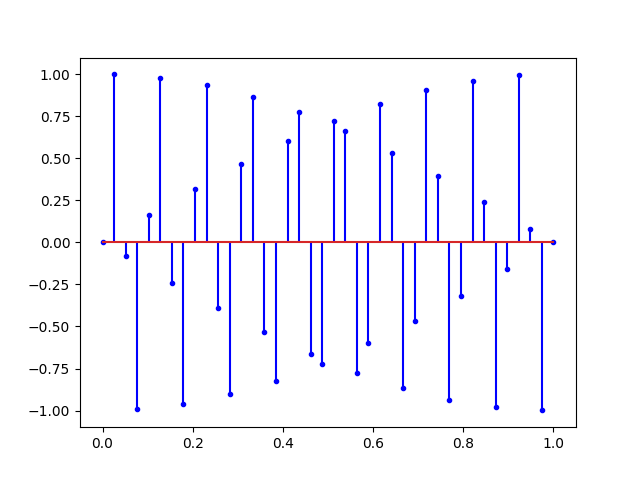
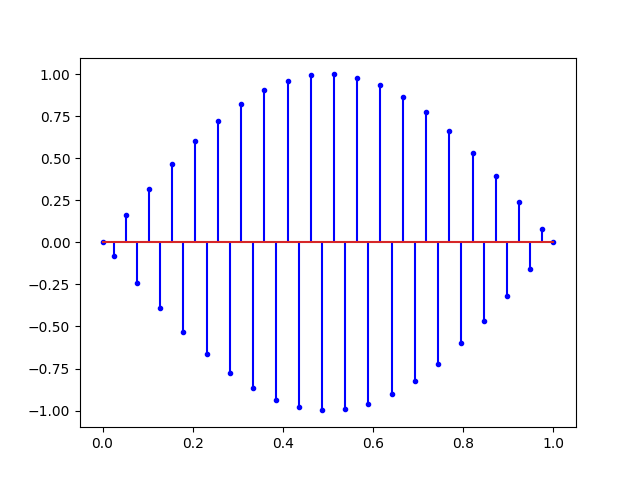
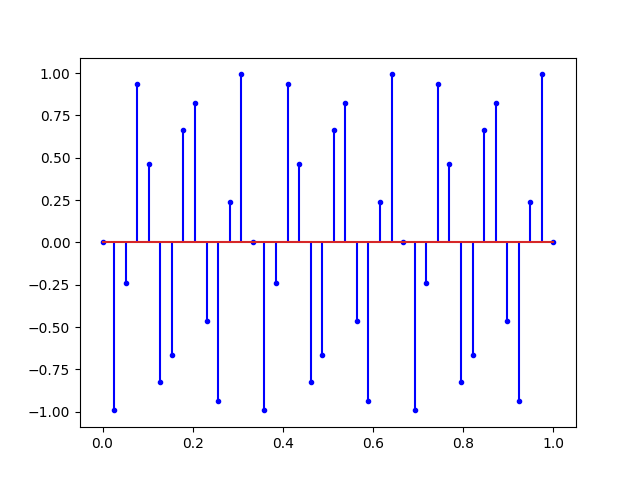
Ce que nous dit Nyquist, c’est qu’avec tous les signaux ci-dessus, il est possible de retrouver la sinusoïde du début. Mais si on augmente encore la fréquence on obtient un repliement du spectre.
On peut ajouter le l’analyse de spectre en augmentant également le nombre de points mesuré :
# Freq
f0 = 1
# Temps total
T = 1
# Nombre de points:
N = 100
# 100 points de 0 à 99
t = np.linspace(0, T, N)
y = np.sin(2*np.pi*f0*t)
fix, ax = plt.subplots(1,2)
ax[0].stem(t, y, 'b', markerfmt="b.")
ax[1].magnitude_spectrum(y, Fs=N/T, ds="steps-mid")
plt.show()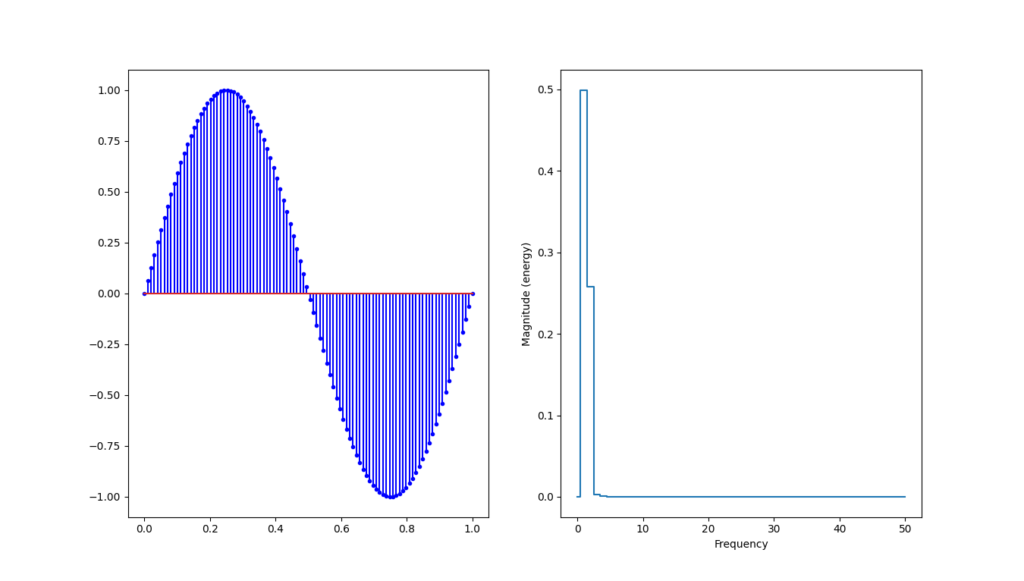
Ondelettes
Pour faire une ondelette (wavelet) on multiplie un cosinus (périodique) avec une gaussienne (exp(-t²/2)) :
# Décalage en seconde:
retard = 5
y = np.cos(2*np.pi*f0*t)*np.exp(-np.power(t-retard,2)/2)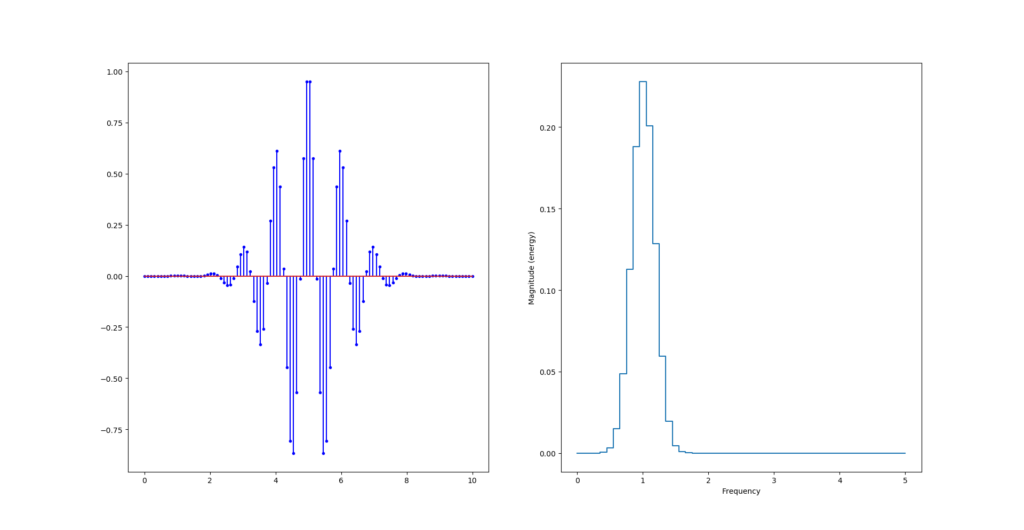
La vidéo suivante explique tout ce que vous avez toujours voulu savoir sur les ondelettes.
Si on change la fréquence du signal, en passant à 2Hz par exemple. On se rend compte que l’échantillonnage tronque les maximum locaux :
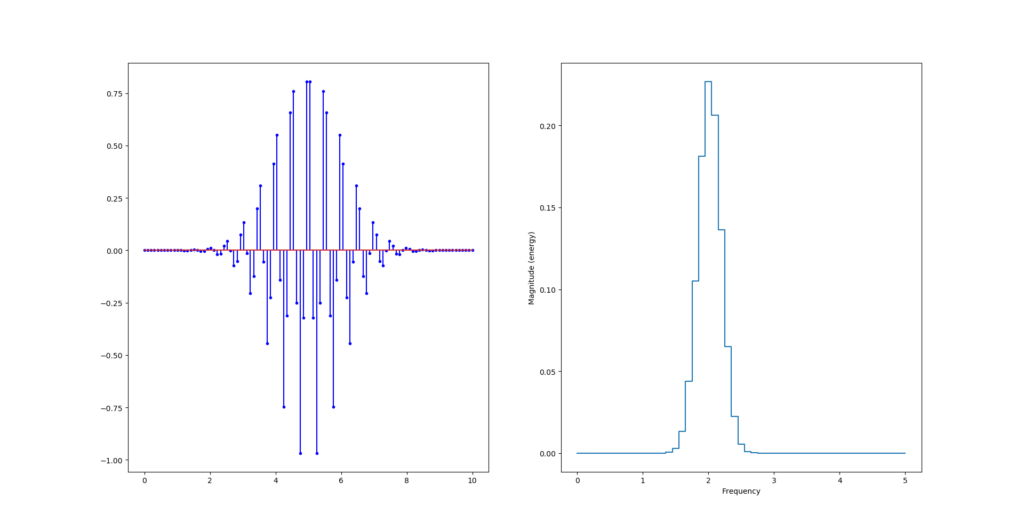
Ce qui casse la symétrie de la courbe.
Hilbert avec scipy
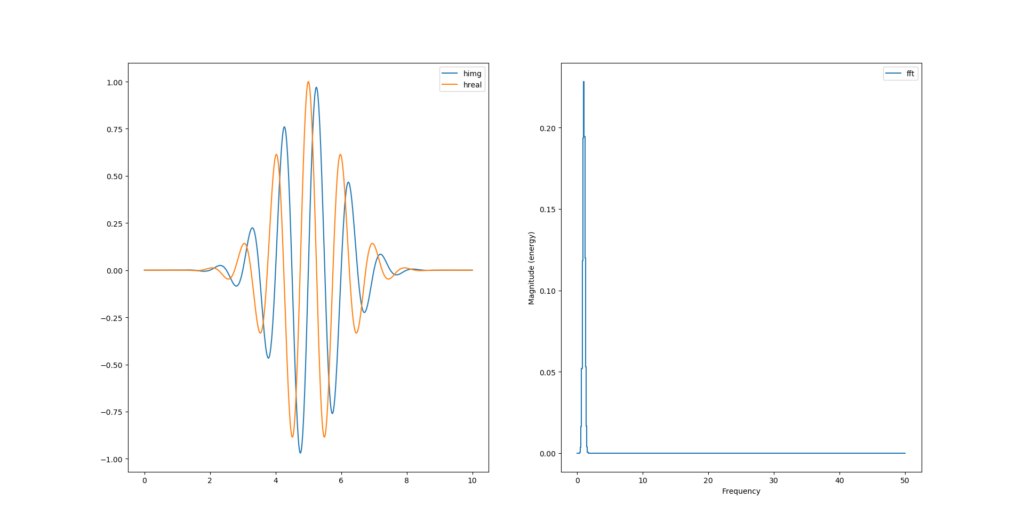
La transformée de hilbert permet de calculer la partie imaginaire du signal réel. Le package python nommé scipy inclue la fonction qui la calcule.
[...]
from scipy import signal
[...]
# morlet wavelet
y = np.cos(2*np.pi*f0*t)*np.exp(-np.power(t-retard,2)/2)
himg = signal.hilbert(y).imag
hreal = signal.hilbert(y).real
[...]
Comme nous avons la partie réelle et la partie imaginaire de notre signal, il est possible désormais de calculer son module pour en tirer l’enveloppe:
# morlet wavelet
y = np.cos(2*np.pi*f0*t)*np.exp(-np.power(t-retard,2)/2)
himg = signal.hilbert(y).imag
hreal = signal.hilbert(y).real
habs = np.sqrt(np.power(himg, 2) + np.power(hreal, 2))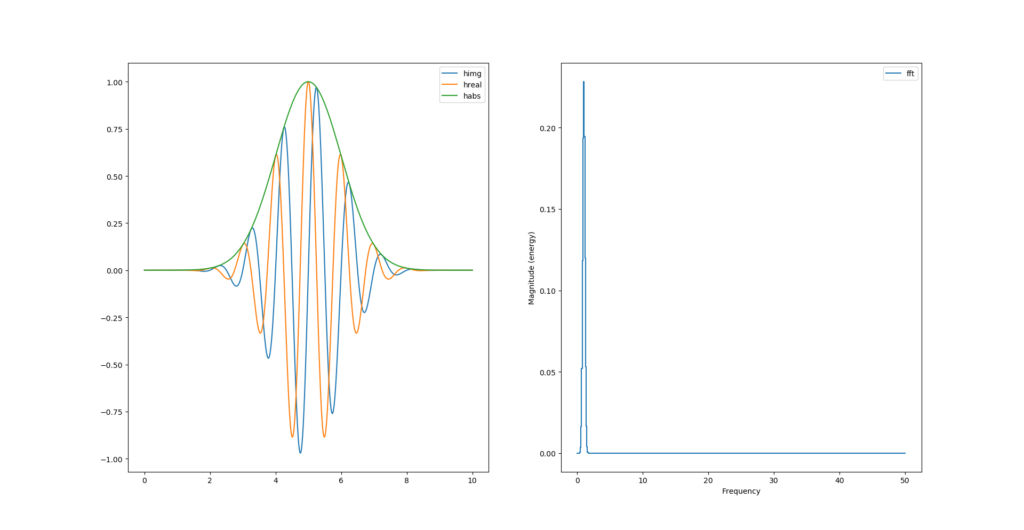
Si l’on diminue la fréquence d’échantillonnage (division par 10) on remarque que l’enveloppe ne passe plus par les maximums. La transformée de Hilbert semble les avoirs tout de même déduit :
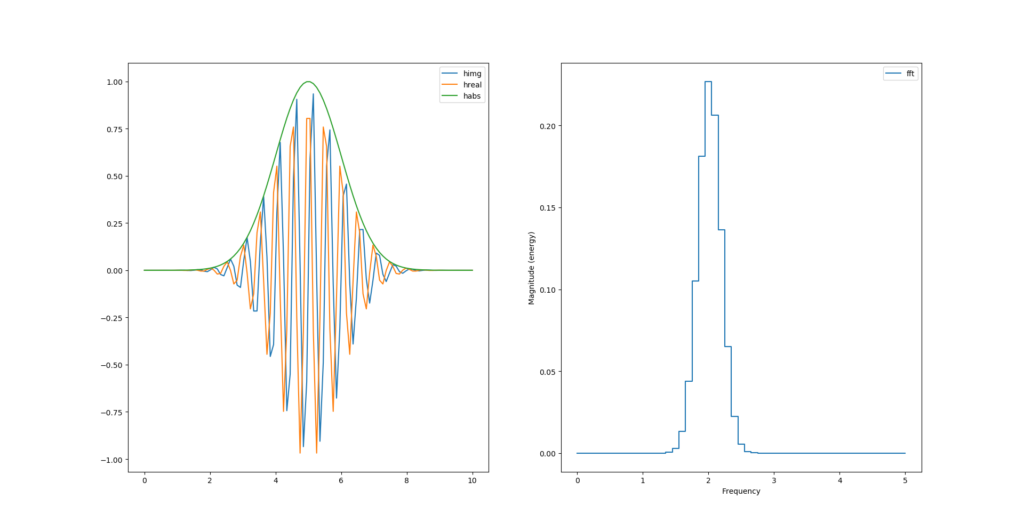
Peut-on calculer l’enveloppe sans racine carré et carré ?
habs = np.abs(himg) + np.abs(hreal)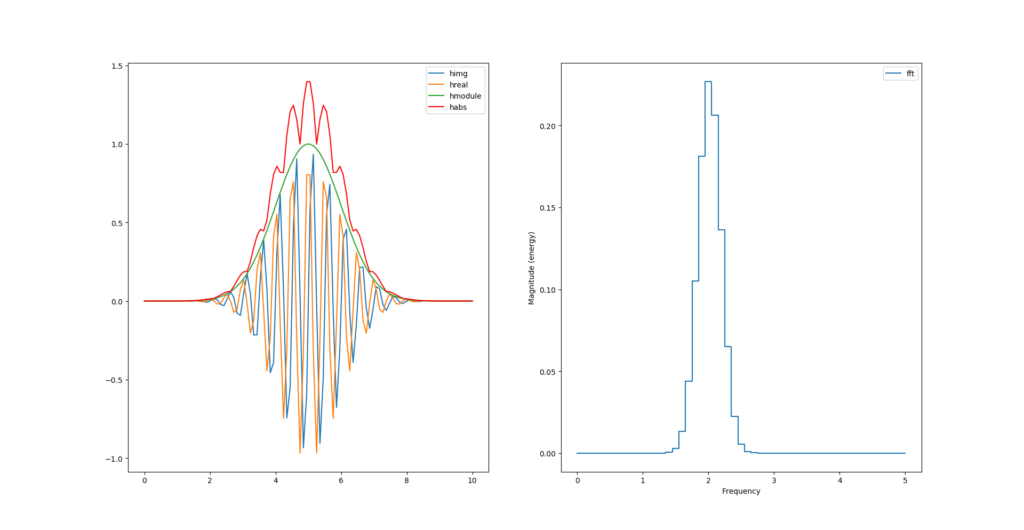
Et juste avec des carrés ?
hsquare= np.power(himg, 2) + np.power(hreal, 2)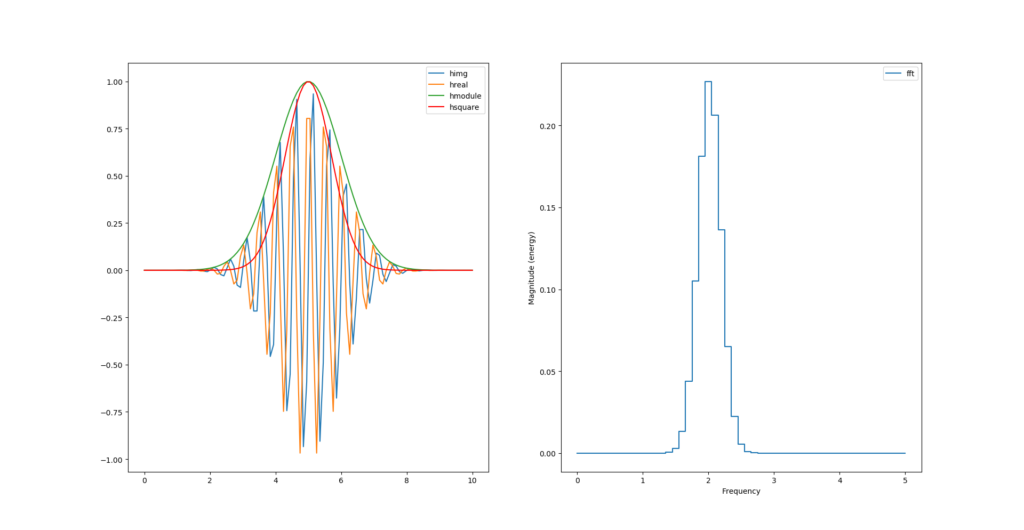
Transformée de Fourrier
Mais que faites vous encore sur ce blog ! Vite allez visionner l’excellente vidéo de 3Blue1Brown qui parle de la transformée de Fourrier avec force de graphes et de dessins. Vous ne verrez plus la transformée de fourrier comme avant 😉
Sinon y a aussi cette formule trouvée sur twitter qui est vraiment très parlante :
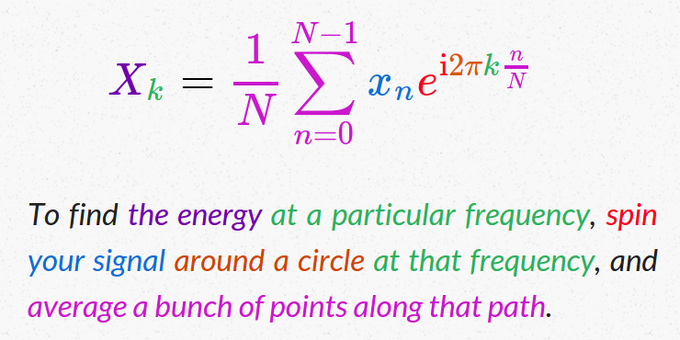
Jusqu’à présent, pour calculer et afficher la transformée de fourrier de notre signal, nous nous sommes servi exclusivement de la fonction magnitude_spectrum() inclue dans pylab. C’est intéressant pour avoir un aperçu du spectre, mais ça ne permet pas de dire que l’on maîtrise ça.
Nombre complexes en python
Python permet visiblement d’utiliser nativement des nombres complexes avec ‘j’ à condition d’y mettre un nombre devant :
In [2]: j
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
<ipython-input-2-3eedd8854d1e> in <module>
----> 1 j
NameError: name 'j' is not defined
In [3]: 1j
Out[3]: 1j
In [4]: 0.02j
Out[4]: 0.02j
In [5]: -3j
Out[5]: (-0-3j)
In [7]: np.exp(1j)
Out[7]: (0.5403023058681398+0.8414709848078965j)
Tentons donc de calculer la transformée de fourrier en mode «brute de force» pour voir:
#temps: 0 points de 0 à N-1
t = np.linspace(0, T, N)
# morlet wavelet
y = np.cos(2*np.pi*f0*t)*np.exp(-np.power(t-retard,2)/2)
# transformée de fourrier
freqs = np.array([])
for k in range(N):
listexp = [y[n]*np.exp(1j*2*np.pi*k*n/N) for n in range(N)]
xk = (1/N)*np.array(listexp).sum()
freqs = np.append(freqs, xk)
#fréquence: 0 points de 0 à N-1
k = np.linspace(0, T, N)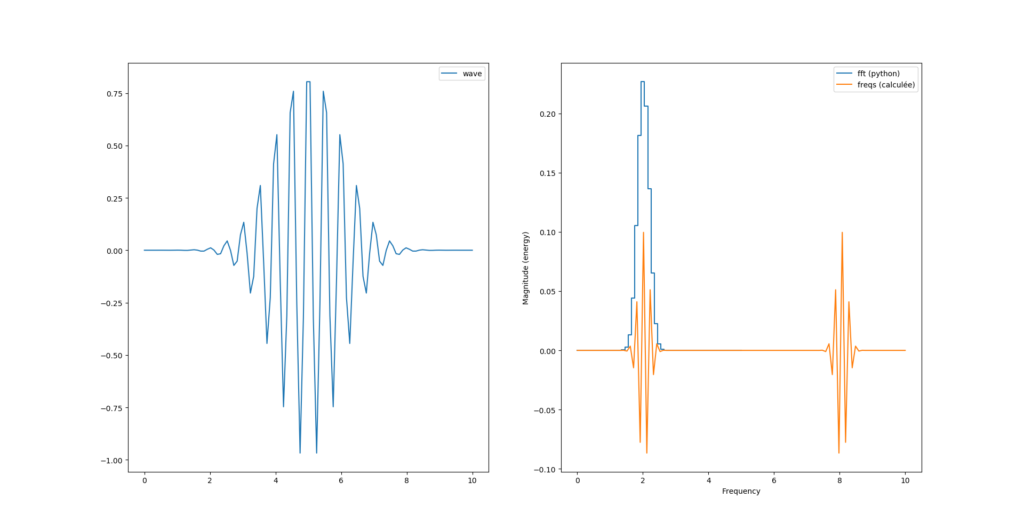
Là ce que nous venons de calculer est la version complexe de la transformée de fourrier dont pylab nous «plot» la partie réelle. Voyons voir le module :
fourrier_module = np.sqrt(np.power(freqs.imag, 2) + np.power(freqs.real, 2))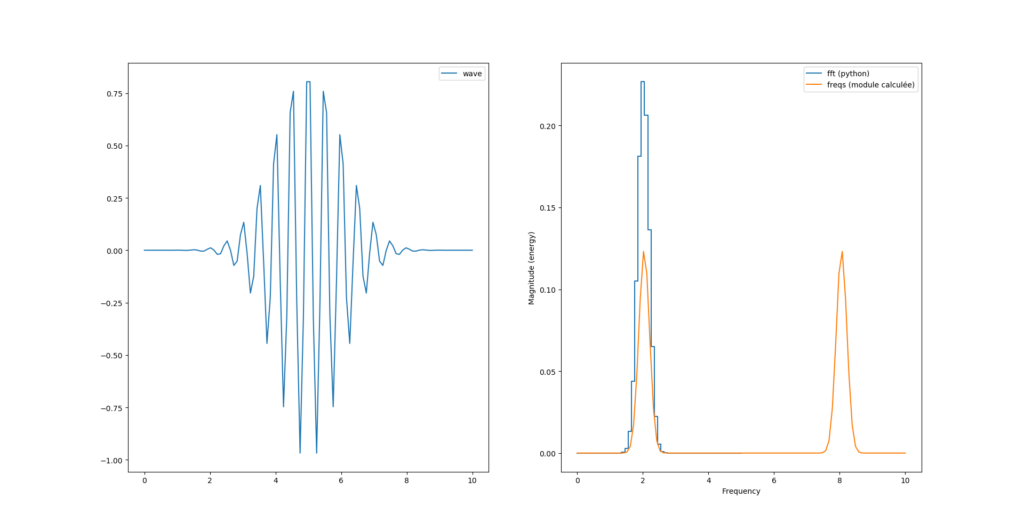
Nous avons donc toujours deux pics, sachant que le second pic est au delà de la fréquence de Nyquist (Fs=10Hz) et semble «normal».
Par contre nous avons un facteur 2 entre le calcul de magnitude de python et celui que l’on vient de calculer.
Peut-être parce que la formule de l’image est celle de la transformée inverse ? La transformée discrète donnée dans le livre est plutôt celle là :
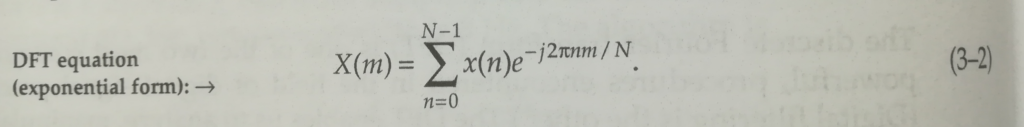
Voyons voir avec cette nouvelle formule :
# transformée de fourrier
freqs = np.array([])
for k in range(N):
listexp = [y[n]*np.exp(-1j*2*np.pi*k*n/N) for n in range(N)]
xk = np.array(listexp).sum()
freqs = np.append(freqs, xk)
fourrier_module = np.sqrt(np.power(freqs.imag, 2) + np.power(freqs.real, 2))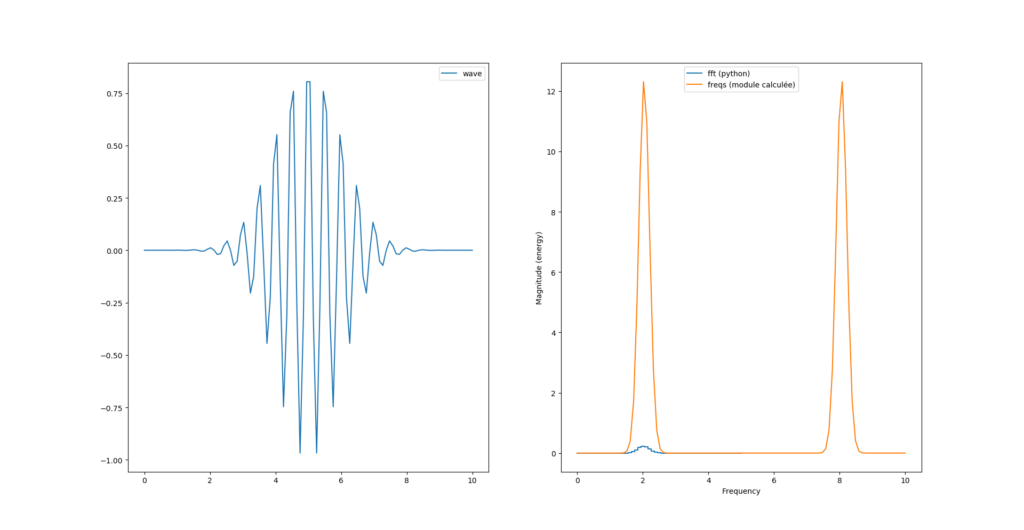
Si on veut «matcher» la courbe de magnitude il faut ajouter un facteur 2/N au calcul du module :
fourrier_module = (2/N)*np.sqrt(np.power(freqs.imag, 2) + np.power(freqs.real, 2))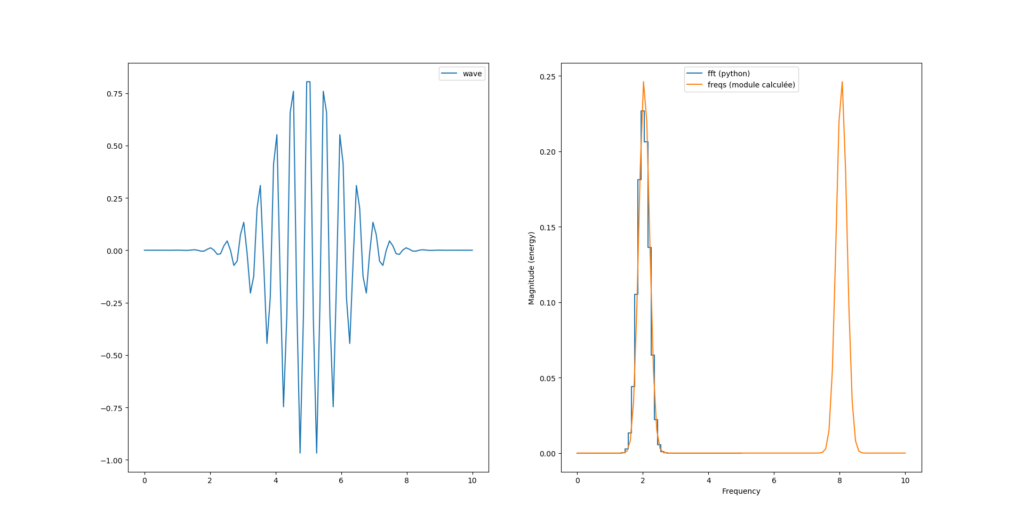
cos – sin
Pour faire entrer le calcul de la transformée dans un FPGA, l’exponentielle d’un complexe n’est pas super pratique. Décomposons donc en différence cos-sin avec la formule d’Euler, on devrait obtenir le même résultat:
# transformée de fourrier
freqs = np.array([])
for k in range(N):
listexp = []
for n in range(N):
angle = 2*np.pi*k*n/N
listexp.append(y[n]*(np.cos(angle) - 1j*np.sin(angle)))
xk = np.array(listexp).sum()
freqs = np.append(freqs, xk)Et nous obtenons exactement le même graphe qu’avant.
C’est sans surprise qu’on obtient la même chose en sommant indépendamment partie réelle et partie imaginaire :
# transformée de fourrier
freqs_real = np.array([])
freqs_img = np.array([])
for k in range(N):
listreal = []
listimg = []
for n in range(N):
angle = 2*np.pi*k*n/N
listreal.append(y[n]*(np.cos(angle)))
listimg.append(y[n]*(-np.sin(angle)))
xkreal = np.array(listreal).sum()
xkimg = np.array(listimg).sum()
freqs_real = np.append(freqs_real, xkreal)
freqs_img = np.append(freqs_img, xkimg)
fourrier_module = (2/N)*np.sqrt(np.power(freqs_img, 2) + np.power(freqs_real, 2))Nous permettant au passage de dégager le ‘j’ des nombres complexes qui ne passe pas très bien dans un FPGA.
Des entiers ou des virgules fixes
Pour le moment c’était facile: on avait les flottant de python. Seulement voilà, dans un FPGA, les flottants ne sont pas simple. Nous avons besoin de fixer la taille (en bits) des variables/registres utilisés. Il faut également fixer la position de la virgule si l’on souhaite simplifier le calcul.
Le second problème nous vient des fonctions sin() et cos() qui ne sont pas calculables simplement. L’astuce consiste à pré-calculer les valeurs et les stocker dans une table qui ira remplir une ROM du FPGA.
Pour gérer des entiers en virgule fixe et de taille hétérogène on installera le module fxpmath :
$ git clone https://github.com/francof2a/fxpmath.git
$ cd fxpmath/
$ python -m pip install -e .Pour commencer on va passer le signal ‘y’ en entier signé sur 16bits avec
# morlet wavelet
y = np.cos(2*np.pi*f0*t)*np.exp(-np.power(t-retard,2)/2)
YTYPE="S1.15"
ysint = Fxp(y, dtype=YTYPE)Le signal se trouvant entre -1 et 1 nous choisirons un format signé sur 16 bits avec tous les chiffres derrière la virgule ‘S1.15’.
Pour les calculs intermédiaires on va rester sur du signé 16 bits mais avec la virgule au milieu cette fois, soit ‘S8.8’:
# transformée de fourrier
freqs_real = np.array([])
freqs_img = np.array([])
for k in range(N):
listreal = []
listimg = []
for n in range(N):
angle = Fxp(2*fixpi*Fxp(k, dtype=DTYPE)*Fxp(n, dtype=DTYPE)/N,
dtype=DTYPE)
listreal.append(Fxp(y[n]*( np.cos(angle)), dtype=DTYPE))
listimg.append (Fxp(y[n]*(-np.sin(angle)), dtype=DTYPE))
xkreal = Fxp(np.array(listreal).sum(), dtype=DTYPE)
xkimg = Fxp(np.array(listimg ).sum(), dtype=DTYPE)
print(f"Freq {k} -> {xkreal}({xkreal.dtype}) + {xkimg}j ({xkimg.dtype})")
freqs_real = np.append(freqs_real, xkreal)
freqs_img = np.append(freqs_img, xkimg)
#fourrier_module = (2/N)*np.sqrt(np.power(freqs_img, 2) + np.power(freqs_real, 2))
fourrier_power = Fxp(Fxp(freqs_img*freqs_img, dtype=DTYPE) + Fxp(freqs_real*freqs_real, dtype=DTYPE), dtype=DTYPE)
fourrier_module = Fxp((2/N)*Fxp(np.sqrt(fourrier_power), dtype=DTYPE), dtype=DTYPE)La première surprise de cette méthode est le temps de calcul: on passe d’un calcul de la transformée quasi instantanée à un calcul qui prend presque une minute.
La seconde surprise vient avec le «bruit haute fréquence» qui apparaît dans le résultat et le second pic qui disparaît.
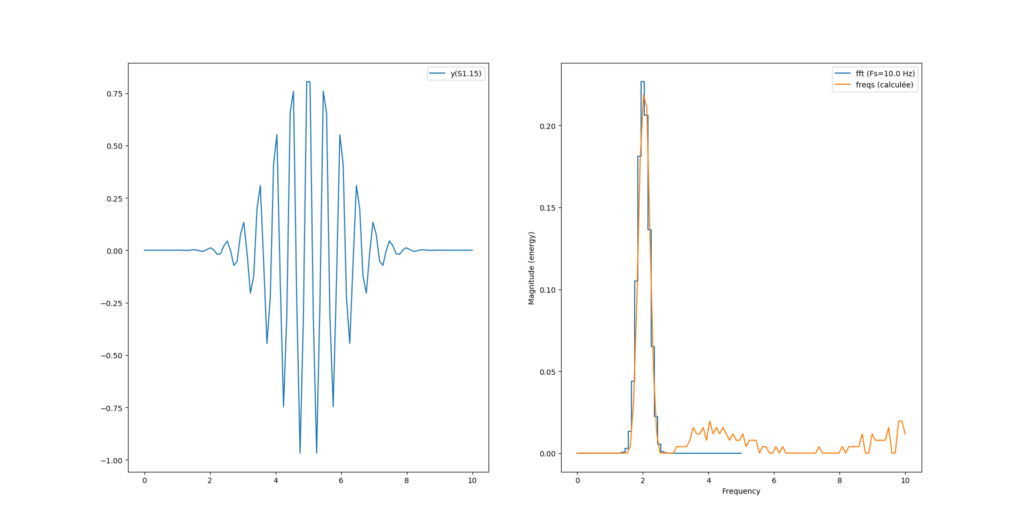
Le problème de ce bruit vient de l’arrondi calculé sur Pi, si on ajuste la virgule de Pi comme ceci :
# Frequence du signal
Sf0 = 2
f0 = (Sf0 * Fs)/T
# Décalage en seconde:
retard = 5
#temps: 0 points de 0 à N-1
t = np.linspace(0, T, N)
# morlet wavelet
y = np.cos(2*np.pi*f0*t)*np.exp(-np.power(t-retard,2)/2)
YTYPE="S1.15"
ysint = Fxp(y, dtype=YTYPE)
DTYPE="S8.8"
D2TYPE="S16.16"
fixpi = Fxp(np.pi, dtype="U3.13")
# transformée de fourrier
freqs_real = np.array([])
freqs_img = np.array([])
for k in range(N):
listreal = []
listimg = []
for n in range(N):
angle = Fxp(2*fixpi*Fxp(k*n, dtype="U16.0")/N, dtype=D2TYPE)
listreal.append(Fxp(y[n], dtype=YTYPE)*Fxp( np.cos(angle), dtype=YTYPE))
listimg.append (Fxp(y[n], dtype=YTYPE)*Fxp(-np.sin(angle), dtype=YTYPE))
xkreal = Fxp(np.array(listreal).sum(), dtype=DTYPE)
xkimg = Fxp(np.array(listimg ).sum(), dtype=DTYPE)
print(f"Freq {k}/{Fs} ({k*T/N}) -> {np.sqrt(xkreal*xkreal + xkimg*xkimg)})")
freqs_real = np.append(freqs_real, xkreal)
freqs_img = np.append(freqs_img, xkimg)
fourrier_power = Fxp(Fxp(freqs_img*freqs_img, dtype=DTYPE) + Fxp(freqs_real*freqs_real, dtype=DTYPE), dtype=DTYPE)
fourrier_module = Fxp((2/N)*Fxp(np.sqrt(fourrier_power), dtype=DTYPE), dtype=DTYPE)
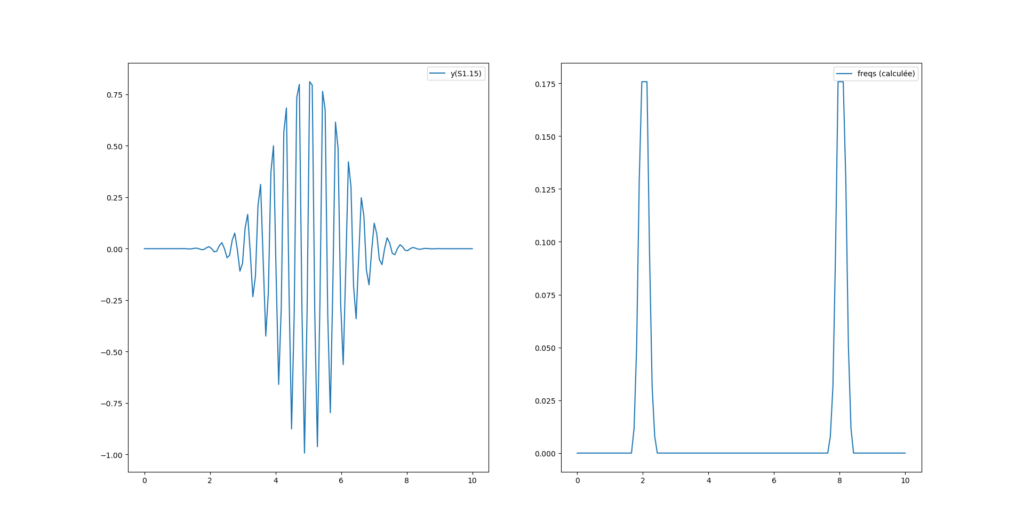
Par contre on a un décalage de fréquence avec la fonction magnitude_spectrum() de pylab :
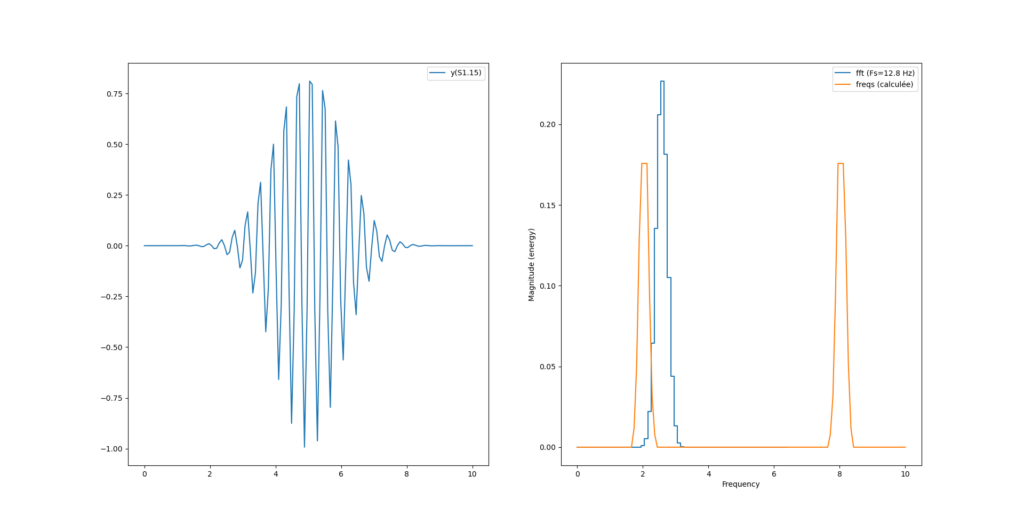
Ce décalage provient de l’axe des x qui n’est pas le même pour le calcul de python et le calcul maison. En effet, notre calcul «à la main» s’étend sur tout l’espace «de nyquist» (0 à N-1) alors que la fonction magnitude_spectrum() n’affiche le spectre que sur la moitée.
Pour recentrer tout ça on peut simplement récupérer la table des fréquences fournie par magnitude_spectrum() et l’utiliser comme axe des x dans l’affichage de notre spectre :
#...
magnitude, freqs, _ = ax[1].magnitude_spectrum(y, Fs=N/T, ds="steps-mid", label=f"fft (Fs={Fs} Hz)")
#...
ax[1].plot(freqs, fourrier_module[:len(freqs)], label = "freqs (calculée)")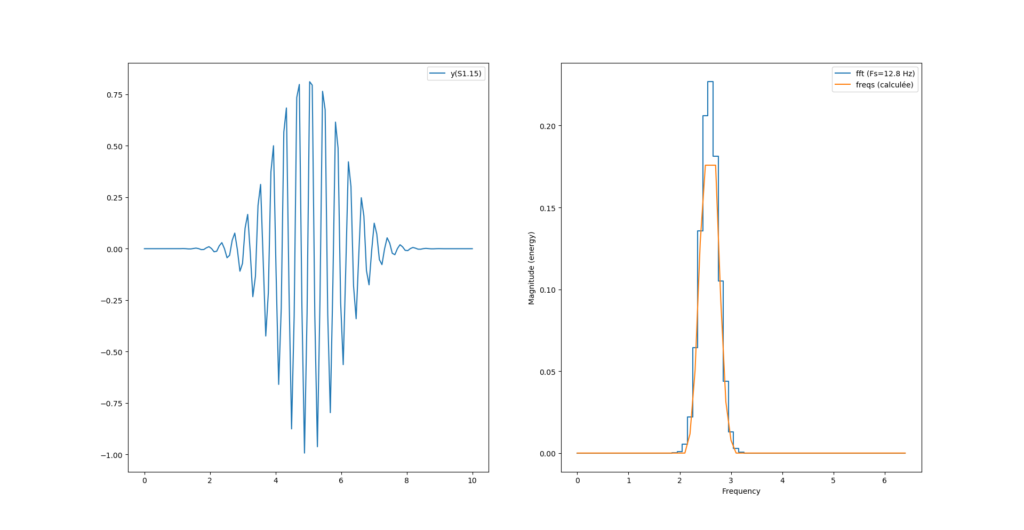
Et nous obtenons la bonne fréquence pour les deux modes de calculs. Reste maintenant un problème de magnitude maximum, est-ce un problème d’arrondi de la virgule fixe ? Possible.
Ressources
Le code de cet article se trouve sur le dépôt github suivant.