Les 10 ans de Cocotb était l’occasion rêvée pour sortir la version 1.8 😉
Archives par mot-clé : python
Et voila, ça fait 10 ans que Cocotb existe. On remercie toute l’équipe du projet qui a ainsi ré-enchanté la validation VHDL/Verilog.
Longue vie à Cocotb \o/
Un timeout dans cocotb
Avec Cocotb nous avons parfois des coroutines qui sont susceptible de rester «coincées» dans une boucle d’attente infinie. Si l’on y prête pas garde, on a vite fait de remplir son disque dur de traces totalement inutile.
# Une coroutine qui attend bien trop longtemps
async def too_long_coroutine(self):
await Timer(1, units="sec")Pour éviter ce problème, l’idéal serait de pouvoir ajouter un «timeout» à l’appel de la coroutine susceptible de bloquer.
Ça tombe bien, cocotb a prévu un trigger pour ça : with_timeout()
from cocotb.triggers import with_timeout
await with_timeout(testcls.too_long_coroutine(), 100, "ns")Sauf que python n’a pas trop l’air d’accord pour exécuter notre coroutine comme un trigger.
TypeError: All triggers must be instances of Trigger! Got: coroutineC’est dommage, on perd beaucoup de l’intérêt de ce trigger !
La solution donnée par marlonjames est d’«empaquetter» la coroutine dans la fonction start_soon() comme ceci :
await with_timeout(
cocotb.start_soon(testcls.too_long_coroutine()),
100, "ns")De cette manière, le test s’interromps sur une levé d’interruption SimTimeoutError et le test est marqué FAIL sans ruiner notre disque dur.
raise cocotb.result.SimTimeoutError
cocotb.result.SimTimeoutErrorSimulons la FFT de Xilinx
Après avoir simulé des FFT avec Python et pylab, voyons comment les intégrer dans un FPGA réel de Xilinx.
Faire une FFT dans un FPGA est quelque chose qui n’est pas trivial. L’avantage, suivant la taille du FPGA, est de pouvoir en faire tourner plusieurs en parallèle pour accélérer le traitement. L’inconvénient étant le temps de développement qui est décuplé par rapport à une solution embarquée sur les habituels DSP ou microcontrôleurs.
Pour accélérer le développement, l’utilisation de modules fournis par les constructeurs est très tentante. Bien sûr, si on utilise la FFT d’un constructeur X, elle ne sera pas utilisable sur le FPGA du constructeur Y… Mais c’est de bonne guerre.
Plus gênant est la difficulté de simuler le module sur son PC pour valider l’algorithme que l’on souhaite mettre en œuvre.
C’est pour cela que Xilinx fournit un modèle C de sa FFT. Modèle que l’on peut utiliser gratuitement avec GCC.
Voyons voir comment mettre tout ça en œuvre.
Installation du modèle
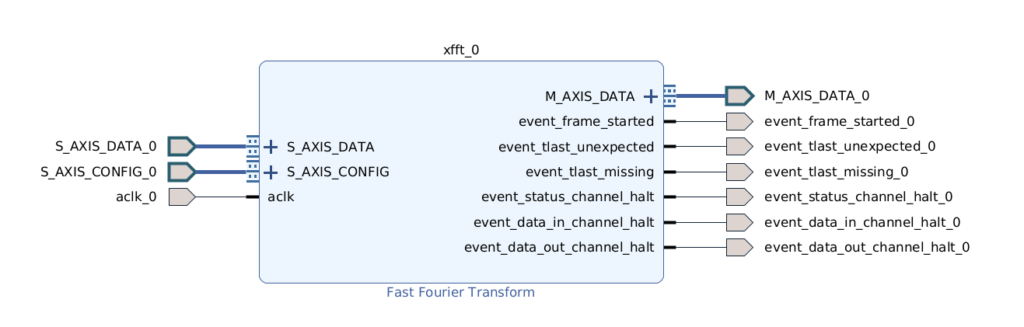
Pour compiler le modèle il faut d’abord le générer à partir d’un projet Vivado. On crée donc un projet Vivado avec un FPGA cible et on instancie le bloc «Fast Fourrier Transform» dans l’«IP designer». Pour pouvoir générer le modèle il faut que les entrées/sorties soient connectées à quelques chose, dans notre cas nous nous contenterons d’exporter les ports.
L’archive au format zip est générée dans le répertoire suivant :
test_fft/test_fft.gen/sources_1/bd/fft_test_design/ip/fft_test_design_xfft_0_0/cmodel/xfft_v9_1_bitacc_cmodel_lin64.zipArchive que l’on dézippera dans le répertoire de son choix :
$ unzip xfft_v9_1_bitacc_cmodel_lin64.zip
$ ls -l
gmp.h
libgmp.so.11
libIp_xfft_v9_1_bitacc_cmodel.so
make_xfft_v9_1_mex.m
run_bitacc_cmodel.c
run_xfft_v9_1_mex.m
xfft_v9_1_bitacc_cmodel.h
xfft_v9_1_bitacc_mex.cppet à laquelle nous ajouterons un fichier main() et un Makefile. Par contre ne rêvez pas, il n’y a pas les sources du modèle 😉 le modèle se trouve dans le fichier binaire de librairie libIp_xfft_v9_1_bitacc_cmodel.so
L’explication pour la compilation est donnée sur le site officiel. Avec g++ ça donne :
$ g++ -std=c++11 -I. -L. -lgmp -Wl,-rpath,. run_bitacc_cmodel.c -o run_fft -lIp_xfft_v9_1_bitacc_cmodelLa compilation génère un binaire nommé run_fft qu’il faut lancer en intégrant les librairies du répertoire courant pour le lien dynamique :
$ LD_LIBRARY_PATH=$$LD_LIBRARY_PATH:. ./run_fft
Running the C model...
Simulation completed successfully
Outputs from simulation are correct
$ Le résultat est relativement frustrant: certes il n’y a pas d’erreur, mais enfin bon … on n’est pas super avancé. On aimerait bien avoir de belles courbes et pouvoir admirer le résultat spectral de cette FFT !
Pour cela il va falloir se plonger dans le code «main()» et injecter son propre signal.
Plongée dans le code
Pour avoir la documentation du modèle on pourra bien sûr se référer à la documentation officiel, mais on peut également se plonger dans le header xfft_v9_1_bitacc_cmodel.h qui est bien commenté.
Le calcul est lancé avec la fonction xilinx_ip_xfft_v9_1_bitacc_simulate déclarée ainsi :
/**
* Simulate this bit-accurate C-Model.
*
* @param state Internal state of this C-Model. State
* may span multiple simulations.
* @param inputs Inputs to this C-Model.
* @param outputs Outputs from this C-Model.
*
* @returns Exit code Zero for SUCCESS, Non-zero otherwise.
*/
Ip_xilinx_ip_xfft_v9_1_DLL
int xilinx_ip_xfft_v9_1_bitacc_simulate
(
struct xilinx_ip_xfft_v9_1_state* state,
struct xilinx_ip_xfft_v9_1_inputs inputs,
struct xilinx_ip_xfft_v9_1_outputs* outputs
);L’état est créé avec la fonction xilinx_ip_xfft_v9_1_create_state() et la structure d’entrée (inputs) possède un tableau de double pour la partie imaginaire et un tableau de double pour la partie réelle. La taille de la FFT étant donnée en 2^n par l’attribut nfft.
struct xilinx_ip_xfft_v9_1_inputs
{
int nfft; //@- log2(point size)
double* xn_re; //@- Input data (real)
int xn_re_size;
double* xn_im; //@- Input data (imaginary)
int xn_im_size;
int* scaling_sch; //@- Scaling schedule
int scaling_sch_size;
int direction; //@- Transform direction
}; // end xilinx_ip_xfft_v9_1_inputsLa structure de sortie est encore plus simple :
struct xilinx_ip_xfft_v9_1_outputs
{
double* xk_re; //@- Output data (real)
int xk_re_size;
double* xk_im; //@- Output data (imaginary)
int xk_im_size;
int blk_exp; //@- Block exponent
int overflow; //@- Overflow occurred
}; // xilinx_ip_xfft_v9_1_outputsDans l’exemple donnée, la partie imaginaire est fixée à 0 sur les 1024 échantillons et la partie réel à 0.5.
// Create input data frame: constant data
double constant_input = 0.5;
int i;
for (i=0; i<samples; i++) {
xn_re[i] = constant_input;
xn_im[i] = 0.0;
}Si le signal est constant, en toute logique seule la fréquence continue (0Hz) doit être différente de 0. C’est ce qui est vérifié après avoir effectué le calcul :
// Check xk_re data: only xk_re[0] should be non-zero
double expected_xk_re_0;
if (C_HAS_SCALING == 0) {
expected_xk_re_0 = constant_input * (1 << C_NFFT_MAX);
} else {
expected_xk_re_0 = constant_input;
}
if (xk_re[0] != expected_xk_re_0) {
cerr << "ERROR:" << channel_text << " xk_re[0] is incorrect: expected " << expected_xk_re_0 << ", actual " << xk_re[0] << endl;
ok = false;
}
for (i=1; i<samples; i++) {
if (xk_re[i] != 0.0) {
cerr << "ERROR:" << channel_text << " xk_re[" << i << "] is incorrect: expected " << 0.0 << ", actual " << xk_re[i] << endl;
ok = false;
}
}
// Check xk_im data: all values should be zero
for (i=1; i<samples; i++) {
if (xk_im[i] != 0.0) {
cerr << "ERROR:" << channel_text << " xk_im[" << i << "] is incorrect: expected " << 0.0 << ", actual " << xk_im[i] << endl;
ok = false;
}
}Transformée de wavelet
Tout ceci n’est pas très parlant pour le moment, testons maintenant le modèle sur la «wavelet» générée à partir d’un script python. Le script permettant de générer le signal et de l’écrire dans un fichier *.txt se trouve dans le répertoire cmodel du dépot github.
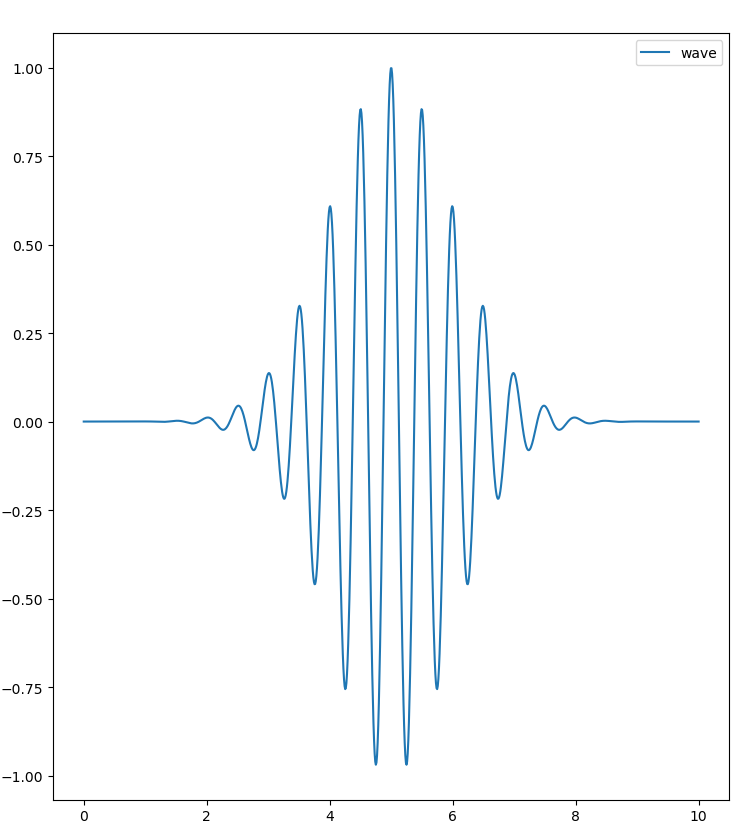
Le script génère un fichier ysig.txt avec toutes les valeurs flottantes écrites en ASCII. On va ensuite relire le fichier avec le programme C++ :
// Read input data from file ysig.txt
std::ifstream yfile; yfile.open("ysig.txt");
if(!yfile.is_open()){
perror("Open error");
exit(EXIT_FAILURE);
}
string line;
int i=0;
while(getline(yfile, line)){
xn_re[i] = stof(line);
cout << stof(line) << endl;
xn_im[i] = 0.0;
i++;
}Le programme écrira le résultat sous dans le fichier xfft_out.txt une fois le résultat calculé:
// save outputs in xfft_out.txt
std::ofstream outfile; outfile.open("xfft_out.txt");
if(outputs.xk_re_size != outputs.xk_im_size){
printf("Error imaginary part size is not equal to real part");
}
for(int i=0; i < outputs.xk_re_size; i++){
outfile << outputs.xk_re[i] << ", " << outputs.xk_im[i] << endl;
}
Fichier que l’on relira pour l’afficher au moyen du script python plot_fft.py
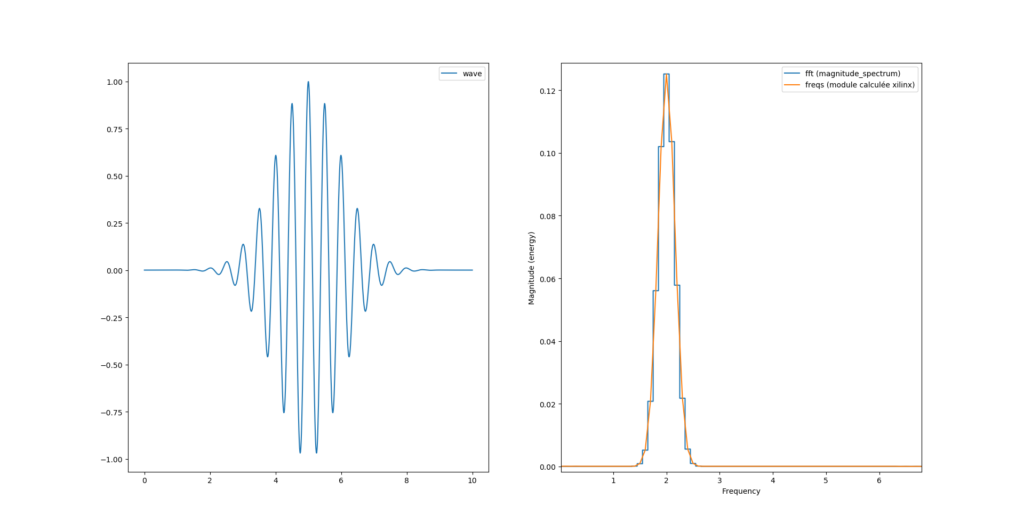
Et nous avons la bonne surprise d’obtenir le même spectre du module qu’avec la fonction de pylab.
On peut maintenant jouer avec les paramètres du module Xilinx et affiner notre modèle de simulation avant de le synthétiser dans un FPGA (de chez Xilinx évidement 😉
Traitement numérique du signal, prise de notes
On dit souvent que pour bien apprendre un sujet en informatique il faut écrire une doc. Pour des besoins pro j’ai du me re-mettre au traitement numérique du signal. Je commence en général par un bouquin et un projet. Pour le projet comme c’est du pro je c’est à ma discrétion, par contre pour le bouquin je me suis plongé dans le livre de Richard G.Lyons «Understanding digital signal processing» qui a le mérite d’être richement illustré de graphes et d’équations avec beaucoup d’explications visuelles et «avec les mains».

L’idée de cette note est donc de faire des exercices en rapport avec ce qui est dans ce livre mais pas que, le tout de manière pratique en python et de voir les implications que ça peut avoir avec les FPGA.
Un signal discret
Dans un premier temps nous aurons besoin de numpy et pylab en python3
import numpy as np
import pylab as pltLe signal de base est une sinusoïde. Pour représenter un signal de 1 Hertz en python on va d’abord créer un tableau d’un certain nombre de valeur de 0 à 1 secondes :
# Freq
f0 = 1
# 40 points de 0 à 39
t = np.linspace(0, 1, 40)Puis calculer le sinus
y = np.sin(2*math.pi*f0*t)Signal qu’il est facile de «plotter» ensuite :
plt.plot(t, y)
plt.show()Ce qui nous donne cette belle courbe de sinus :
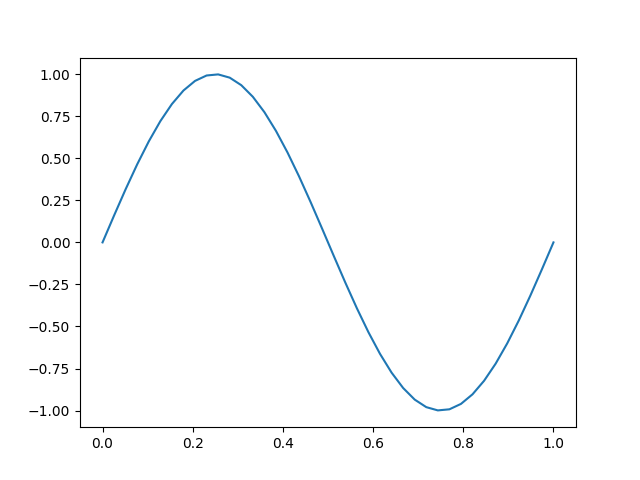
Mais pour bien se représenter un signal numérique il ne faut pas relier les points. Il vaut mieux mettre des points avec des lignes verticales comme ceci :
fix, ax = plt.subplots()
ax.stem(t, y, 'b', markerfmt="b.")
plt.show()Ce qui nous donne la figure suivante :
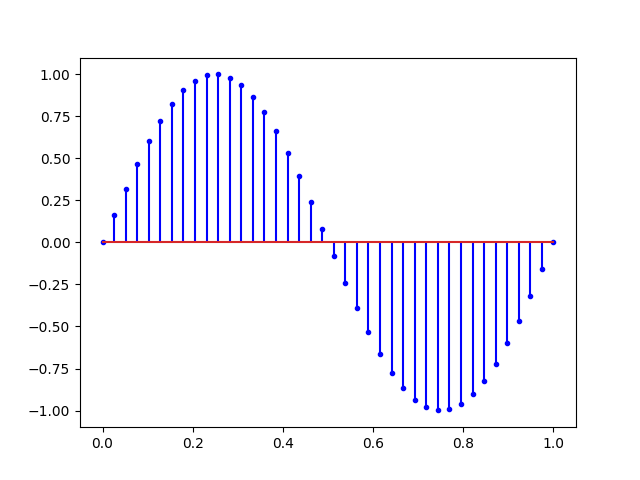
Cette dernière figure illustre bien la notion d’échantillonnage avec une fréquence d’échantillonnage fs de 40Hertz (temps en secondes et 40 points) soit :
# Freq
f0 = 1
# Temps total
T = 1
# Nombre de points:
N = 40
# Fréquence d’échantillonnage :
print(f"fs = {N/T} Hertz")
# fs = 40.0 HertzIci, la fréquence d’échantillonnage (40Hertz) est largement supérieur à la fréquence du signal enregistré (1 Hertz). On peut s’amuser maintenant à monter la fréquence du signal à la fréquence de Nyquist :
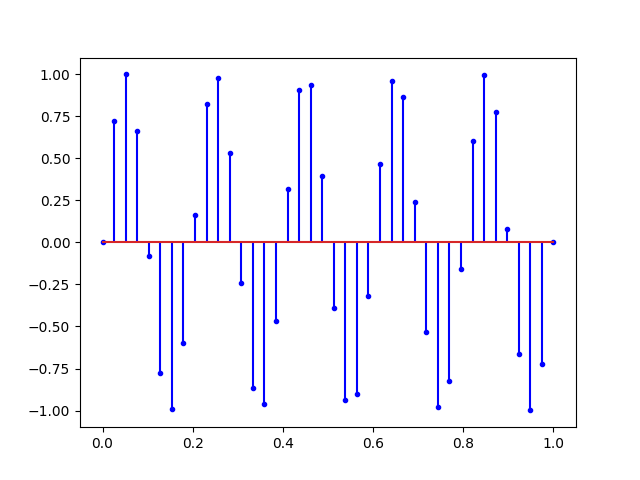
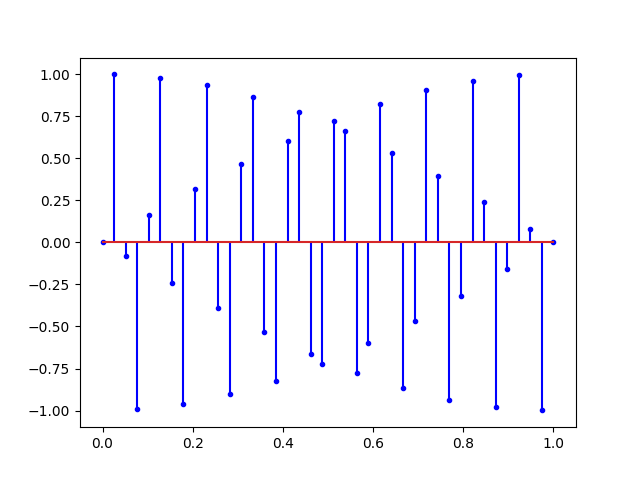
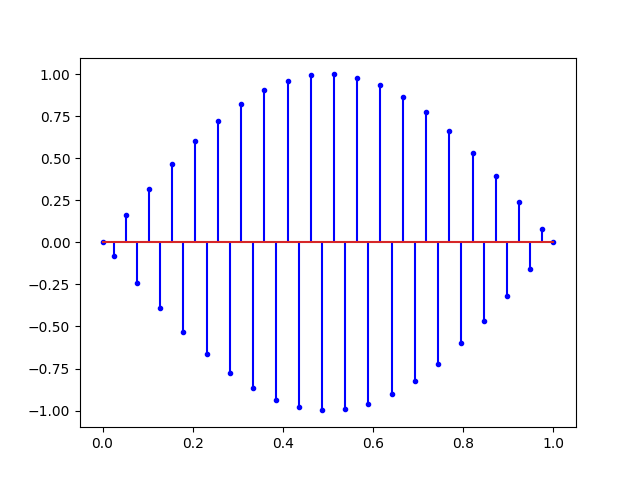
Ce que nous dit Nyquist, c’est qu’avec tous les signaux ci-dessus, il est possible de retrouver la sinusoïde du début. Mais si on augmente encore la fréquence on obtient un repliement du spectre.
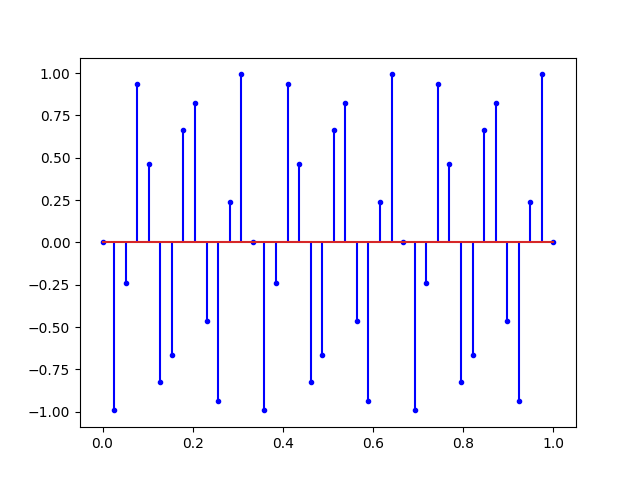
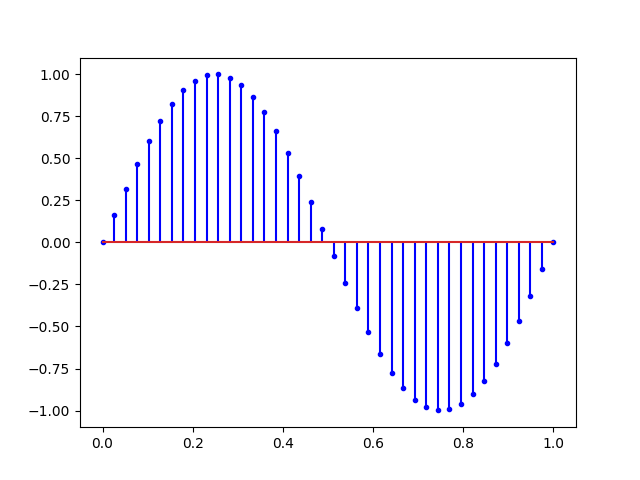
On peut ajouter le l’analyse de spectre en augmentant également le nombre de points mesuré :
# Freq
f0 = 1
# Temps total
T = 1
# Nombre de points:
N = 100
# 100 points de 0 à 99
t = np.linspace(0, T, N)
y = np.sin(2*np.pi*f0*t)
fix, ax = plt.subplots(1,2)
ax[0].stem(t, y, 'b', markerfmt="b.")
ax[1].magnitude_spectrum(y, Fs=N/T, ds="steps-mid")
plt.show()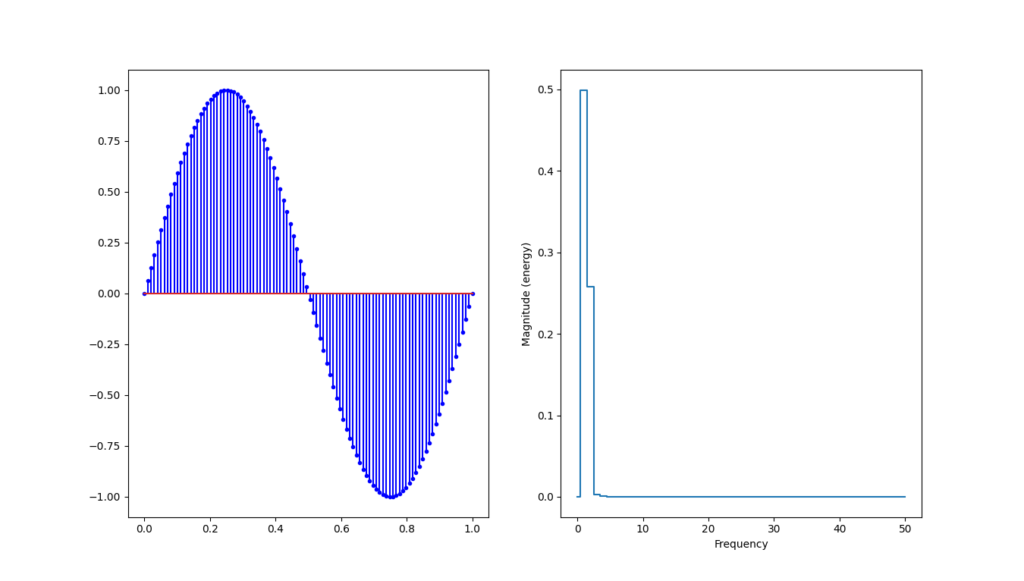
Ondelettes
Pour faire une ondelette (wavelet) on multiplie un cosinus (périodique) avec une gaussienne (exp(-t²/2)) :
# Décalage en seconde:
retard = 5
y = np.cos(2*np.pi*f0*t)*np.exp(-np.power(t-retard,2)/2)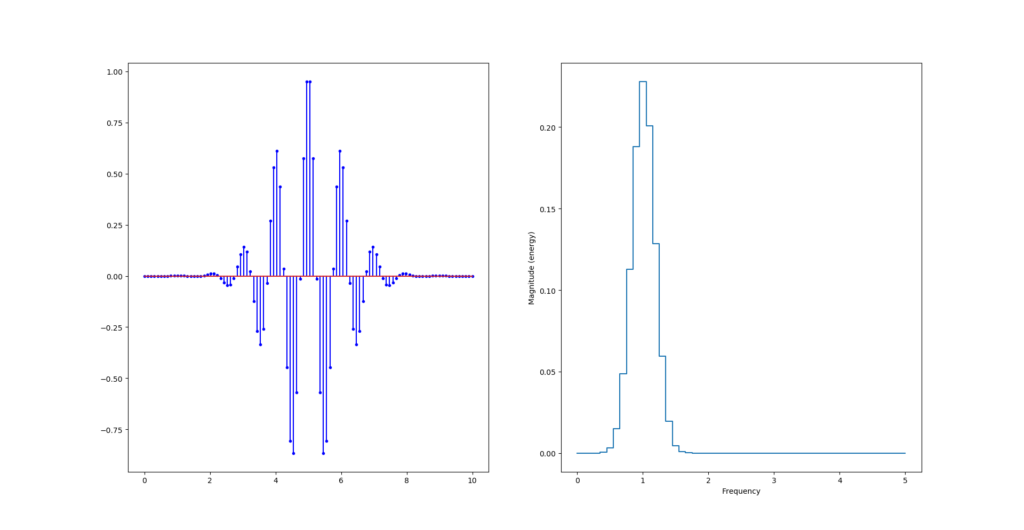
La vidéo suivante explique tout ce que vous avez toujours voulu savoir sur les ondelettes.
Si on change la fréquence du signal, en passant à 2Hz par exemple. On se rend compte que l’échantillonnage tronque les maximum locaux :
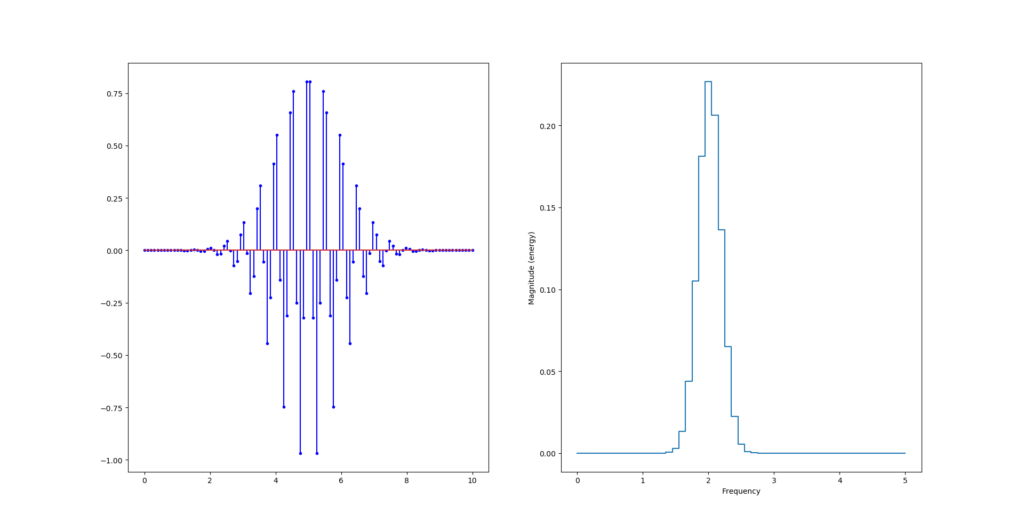
Ce qui casse la symétrie de la courbe.
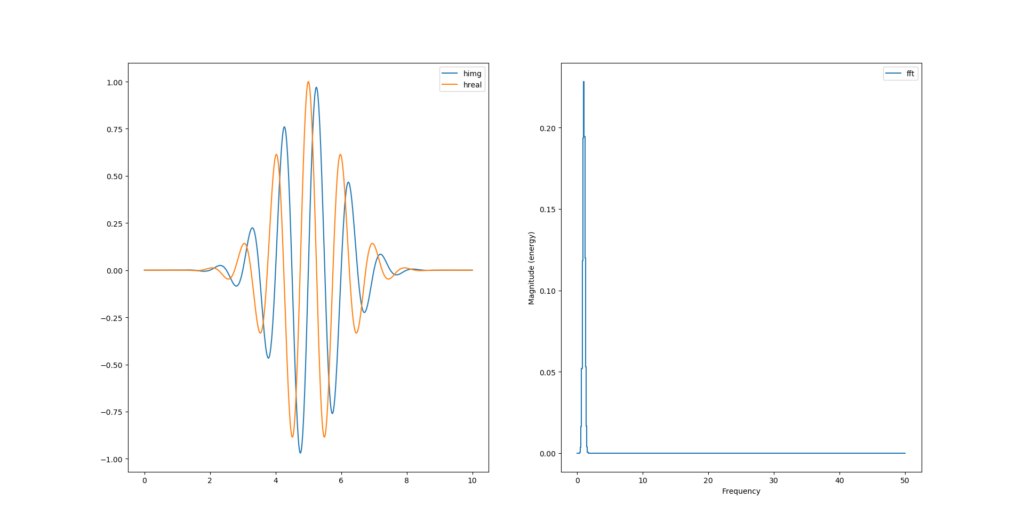
Hilbert avec scipy
La transformée de hilbert permet de calculer la partie imaginaire du signal réel. Le package python nommé scipy inclue la fonction qui la calcule.
[...]
from scipy import signal
[...]
# morlet wavelet
y = np.cos(2*np.pi*f0*t)*np.exp(-np.power(t-retard,2)/2)
himg = signal.hilbert(y).imag
hreal = signal.hilbert(y).real
[...]
Comme nous avons la partie réelle et la partie imaginaire de notre signal, il est possible désormais de calculer son module pour en tirer l’enveloppe:
# morlet wavelet
y = np.cos(2*np.pi*f0*t)*np.exp(-np.power(t-retard,2)/2)
himg = signal.hilbert(y).imag
hreal = signal.hilbert(y).real
habs = np.sqrt(np.power(himg, 2) + np.power(hreal, 2))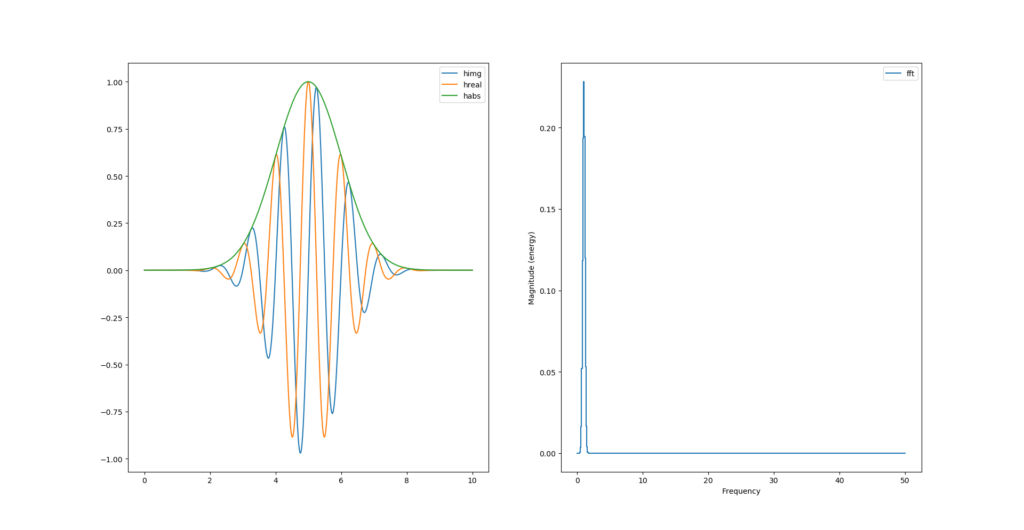
Si l’on diminue la fréquence d’échantillonnage (division par 10) on remarque que l’enveloppe ne passe plus par les maximums. La transformée de Hilbert semble les avoirs tout de même déduit :
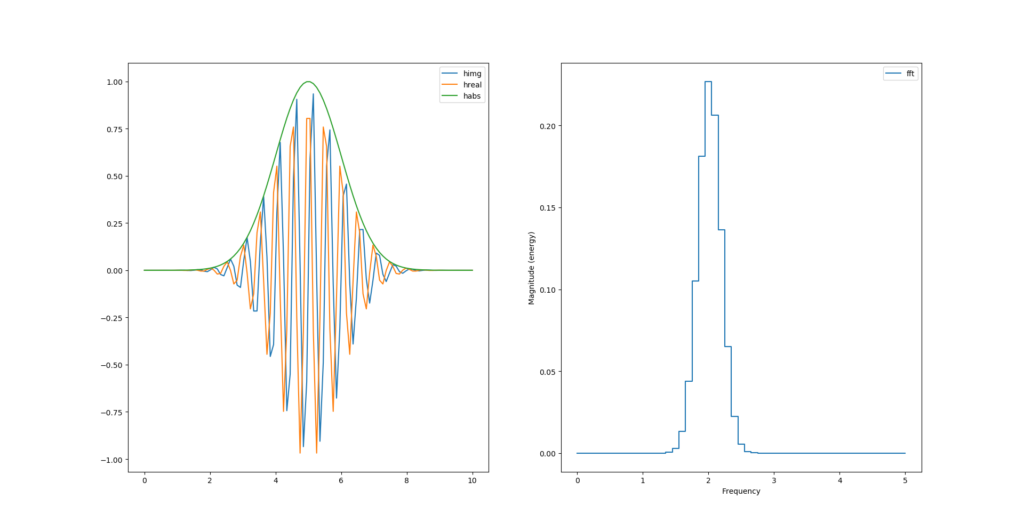
Peut-on calculer l’enveloppe sans racine carré et carré ?
habs = np.abs(himg) + np.abs(hreal)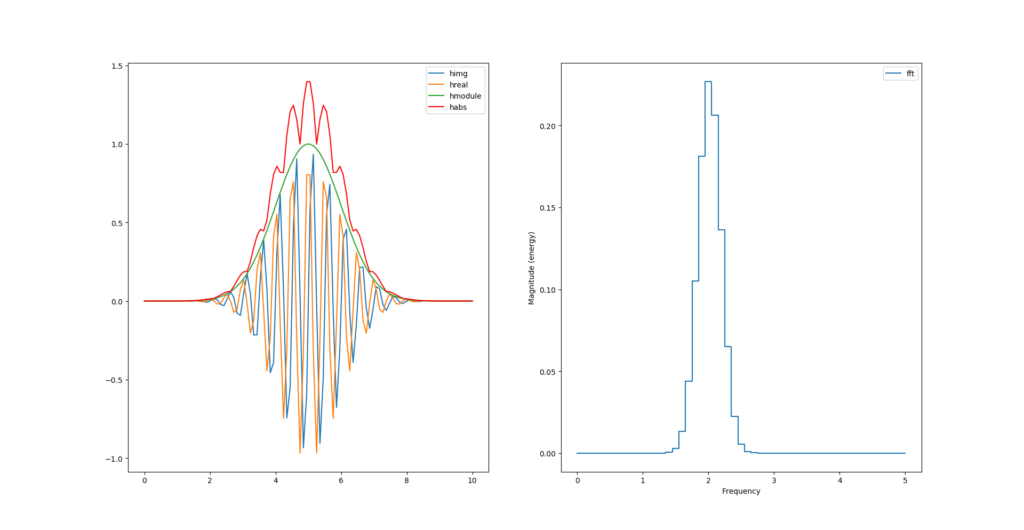
Et juste avec des carrés ?
hsquare= np.power(himg, 2) + np.power(hreal, 2)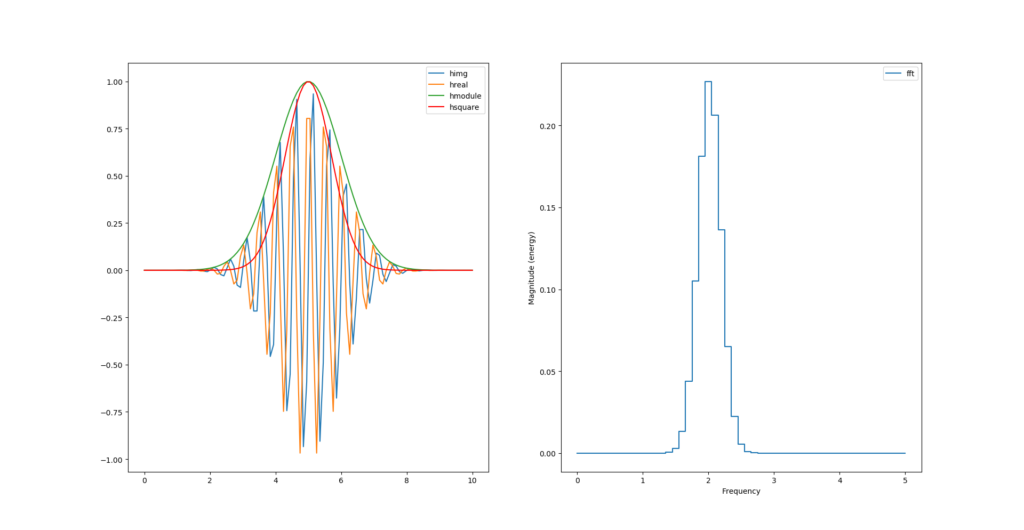
Transformée de Fourrier
Mais que faites vous encore sur ce blog ! Vite allez visionner l’excellente vidéo de 3Blue1Brown qui parle de la transformée de Fourrier avec force de graphes et de dessins. Vous ne verrez plus la transformée de fourrier comme avant 😉
Sinon y a aussi cette formule trouvée sur twitter qui est vraiment très parlante :
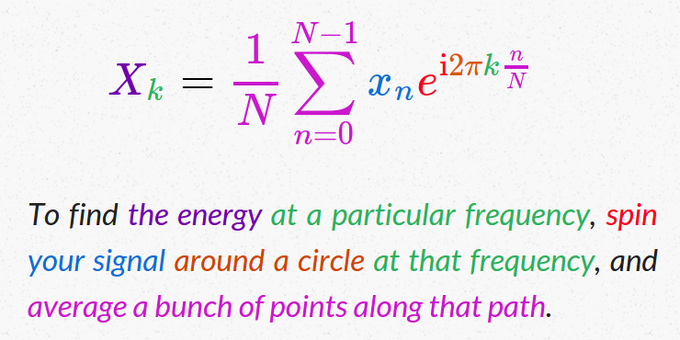
Jusqu’à présent, pour calculer et afficher la transformée de fourrier de notre signal, nous nous sommes servi exclusivement de la fonction magnitude_spectrum() inclue dans pylab. C’est intéressant pour avoir un aperçu du spectre, mais ça ne permet pas de dire que l’on maîtrise ça.
Nombre complexes en python
Python permet visiblement d’utiliser nativement des nombres complexes avec ‘j’ à condition d’y mettre un nombre devant :
In [2]: j
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
<ipython-input-2-3eedd8854d1e> in <module>
----> 1 j
NameError: name 'j' is not defined
In [3]: 1j
Out[3]: 1j
In [4]: 0.02j
Out[4]: 0.02j
In [5]: -3j
Out[5]: (-0-3j)
In [7]: np.exp(1j)
Out[7]: (0.5403023058681398+0.8414709848078965j)
Tentons donc de calculer la transformée de fourrier en mode «brute de force» pour voir:
#temps: 0 points de 0 à N-1
t = np.linspace(0, T, N)
# morlet wavelet
y = np.cos(2*np.pi*f0*t)*np.exp(-np.power(t-retard,2)/2)
# transformée de fourrier
freqs = np.array([])
for k in range(N):
listexp = [y[n]*np.exp(1j*2*np.pi*k*n/N) for n in range(N)]
xk = (1/N)*np.array(listexp).sum()
freqs = np.append(freqs, xk)
#fréquence: 0 points de 0 à N-1
k = np.linspace(0, T, N)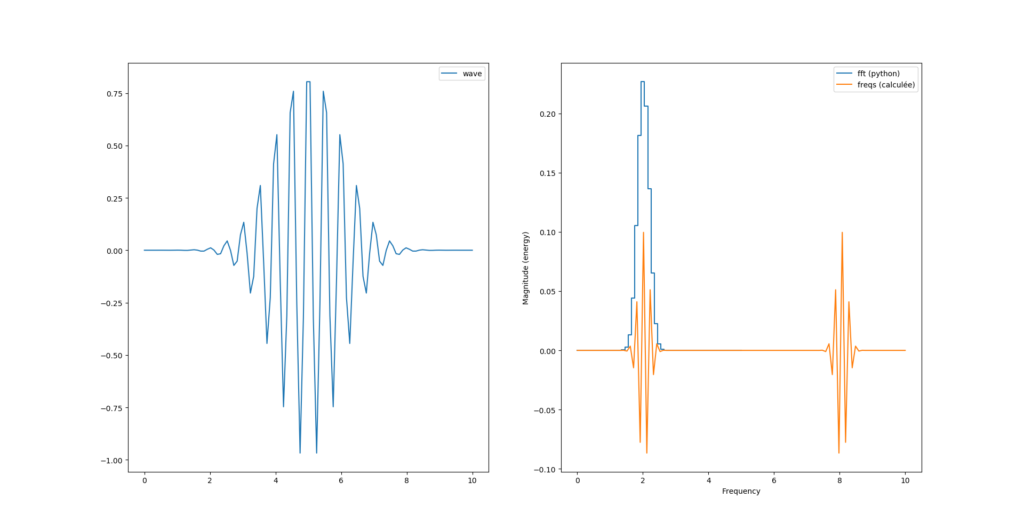
Là ce que nous venons de calculer est la version complexe de la transformée de fourrier dont pylab nous «plot» la partie réelle. Voyons voir le module :
fourrier_module = np.sqrt(np.power(freqs.imag, 2) + np.power(freqs.real, 2))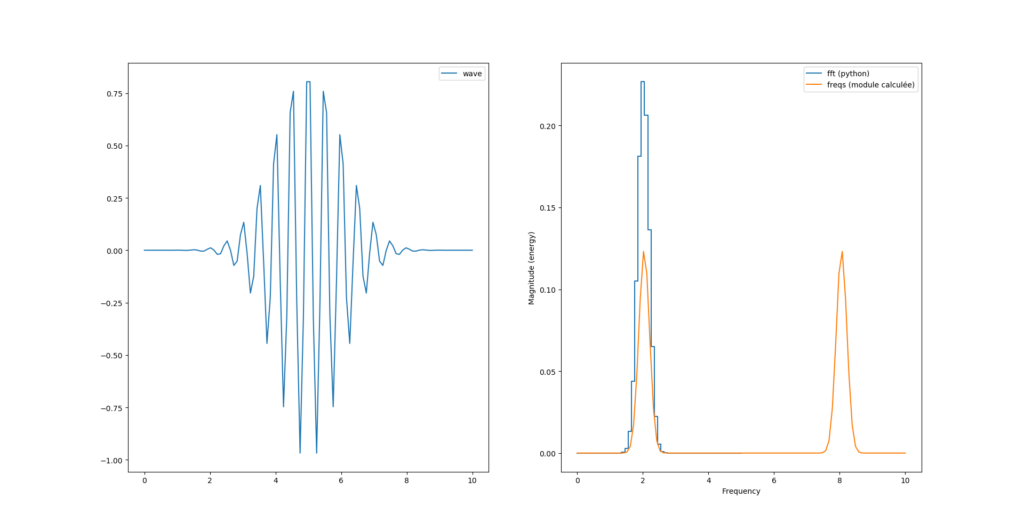
Nous avons donc toujours deux pics, sachant que le second pic est au delà de la fréquence de Nyquist (Fs=10Hz) et semble «normal».
Par contre nous avons un facteur 2 entre le calcul de magnitude de python et celui que l’on vient de calculer.
Peut-être parce que la formule de l’image est celle de la transformée inverse ? La transformée discrète donnée dans le livre est plutôt celle là :
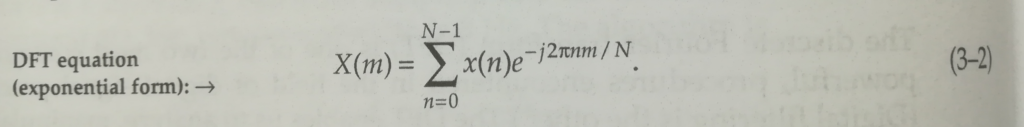
Voyons voir avec cette nouvelle formule :
# transformée de fourrier
freqs = np.array([])
for k in range(N):
listexp = [y[n]*np.exp(-1j*2*np.pi*k*n/N) for n in range(N)]
xk = np.array(listexp).sum()
freqs = np.append(freqs, xk)
fourrier_module = np.sqrt(np.power(freqs.imag, 2) + np.power(freqs.real, 2))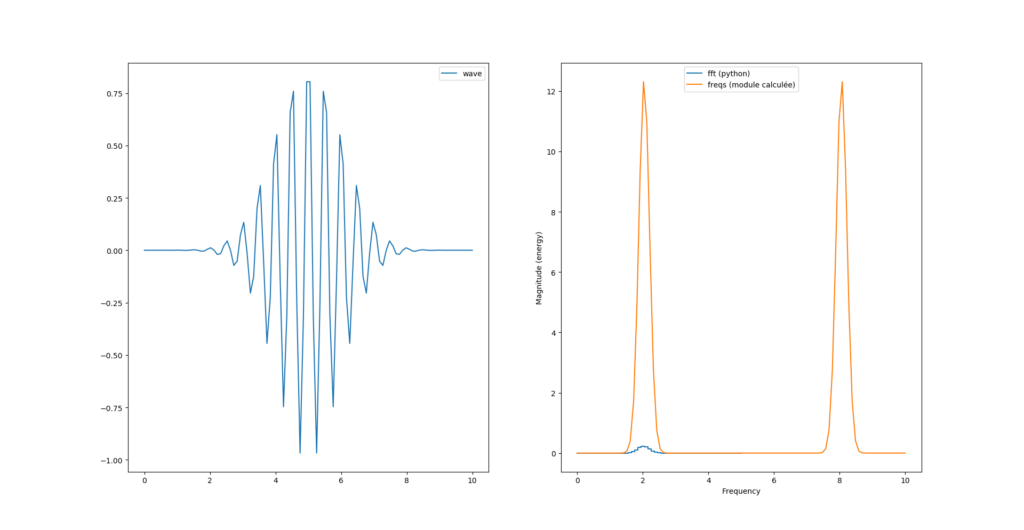
Si on veut «matcher» la courbe de magnitude il faut ajouter un facteur 2/N au calcul du module :
fourrier_module = (2/N)*np.sqrt(np.power(freqs.imag, 2) + np.power(freqs.real, 2))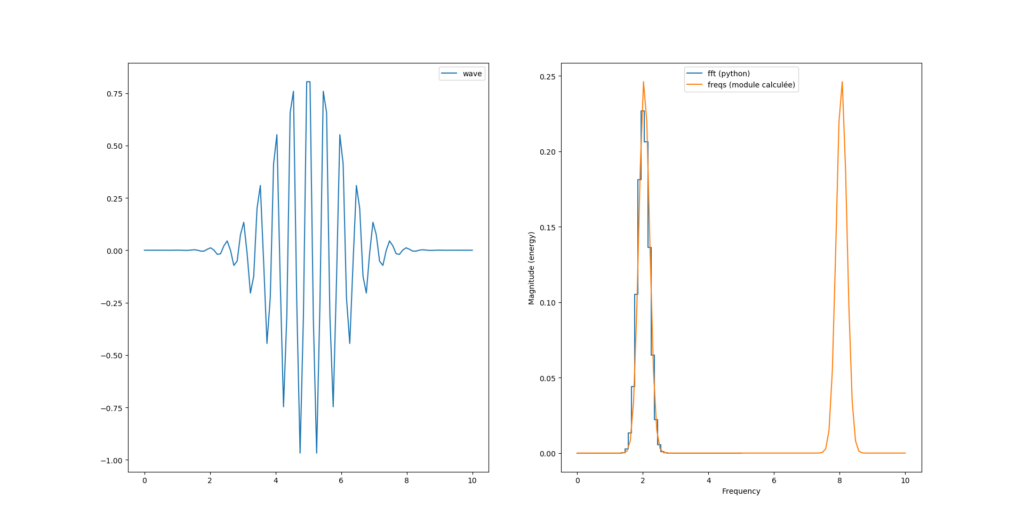
cos – sin
Pour faire entrer le calcul de la transformée dans un FPGA, l’exponentielle d’un complexe n’est pas super pratique. Décomposons donc en différence cos-sin avec la formule d’Euler, on devrait obtenir le même résultat:
# transformée de fourrier
freqs = np.array([])
for k in range(N):
listexp = []
for n in range(N):
angle = 2*np.pi*k*n/N
listexp.append(y[n]*(np.cos(angle) - 1j*np.sin(angle)))
xk = np.array(listexp).sum()
freqs = np.append(freqs, xk)Et nous obtenons exactement le même graphe qu’avant.
C’est sans surprise qu’on obtient la même chose en sommant indépendamment partie réelle et partie imaginaire :
# transformée de fourrier
freqs_real = np.array([])
freqs_img = np.array([])
for k in range(N):
listreal = []
listimg = []
for n in range(N):
angle = 2*np.pi*k*n/N
listreal.append(y[n]*(np.cos(angle)))
listimg.append(y[n]*(-np.sin(angle)))
xkreal = np.array(listreal).sum()
xkimg = np.array(listimg).sum()
freqs_real = np.append(freqs_real, xkreal)
freqs_img = np.append(freqs_img, xkimg)
fourrier_module = (2/N)*np.sqrt(np.power(freqs_img, 2) + np.power(freqs_real, 2))Nous permettant au passage de dégager le ‘j’ des nombres complexes qui ne passe pas très bien dans un FPGA.
Des entiers ou des virgules fixes
Pour le moment c’était facile: on avait les flottant de python. Seulement voilà, dans un FPGA, les flottants ne sont pas simple. Nous avons besoin de fixer la taille (en bits) des variables/registres utilisés. Il faut également fixer la position de la virgule si l’on souhaite simplifier le calcul.
Le second problème nous vient des fonctions sin() et cos() qui ne sont pas calculables simplement. L’astuce consiste à pré-calculer les valeurs et les stocker dans une table qui ira remplir une ROM du FPGA.
Pour gérer des entiers en virgule fixe et de taille hétérogène on installera le module fxpmath :
$ git clone https://github.com/francof2a/fxpmath.git
$ cd fxpmath/
$ python -m pip install -e .Pour commencer on va passer le signal ‘y’ en entier signé sur 16bits avec
# morlet wavelet
y = np.cos(2*np.pi*f0*t)*np.exp(-np.power(t-retard,2)/2)
YTYPE="S1.15"
ysint = Fxp(y, dtype=YTYPE)Le signal se trouvant entre -1 et 1 nous choisirons un format signé sur 16 bits avec tous les chiffres derrière la virgule ‘S1.15’.
Pour les calculs intermédiaires on va rester sur du signé 16 bits mais avec la virgule au milieu cette fois, soit ‘S8.8’:
# transformée de fourrier
freqs_real = np.array([])
freqs_img = np.array([])
for k in range(N):
listreal = []
listimg = []
for n in range(N):
angle = Fxp(2*fixpi*Fxp(k, dtype=DTYPE)*Fxp(n, dtype=DTYPE)/N,
dtype=DTYPE)
listreal.append(Fxp(y[n]*( np.cos(angle)), dtype=DTYPE))
listimg.append (Fxp(y[n]*(-np.sin(angle)), dtype=DTYPE))
xkreal = Fxp(np.array(listreal).sum(), dtype=DTYPE)
xkimg = Fxp(np.array(listimg ).sum(), dtype=DTYPE)
print(f"Freq {k} -> {xkreal}({xkreal.dtype}) + {xkimg}j ({xkimg.dtype})")
freqs_real = np.append(freqs_real, xkreal)
freqs_img = np.append(freqs_img, xkimg)
#fourrier_module = (2/N)*np.sqrt(np.power(freqs_img, 2) + np.power(freqs_real, 2))
fourrier_power = Fxp(Fxp(freqs_img*freqs_img, dtype=DTYPE) + Fxp(freqs_real*freqs_real, dtype=DTYPE), dtype=DTYPE)
fourrier_module = Fxp((2/N)*Fxp(np.sqrt(fourrier_power), dtype=DTYPE), dtype=DTYPE)La première surprise de cette méthode est le temps de calcul: on passe d’un calcul de la transformée quasi instantanée à un calcul qui prend presque une minute.
La seconde surprise vient avec le «bruit haute fréquence» qui apparaît dans le résultat et le second pic qui disparaît.
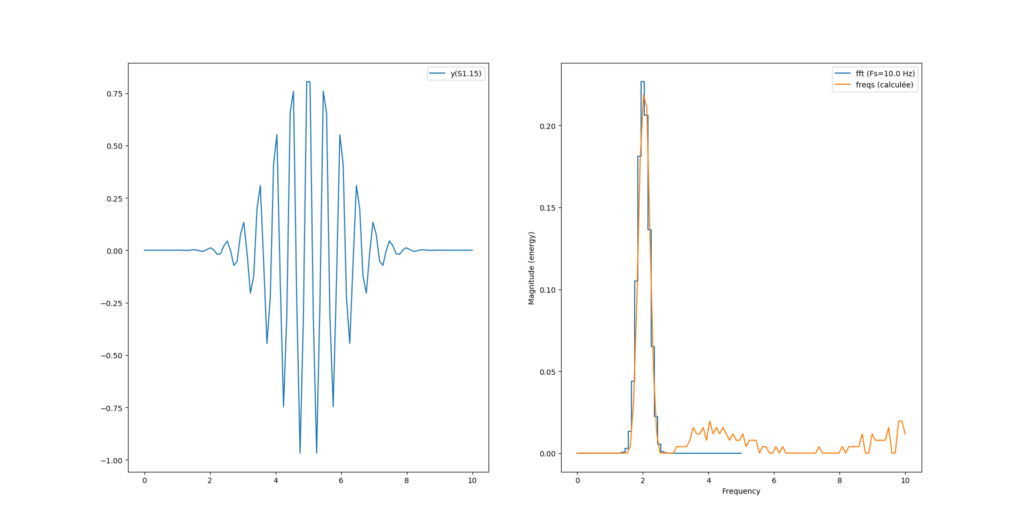
Le problème de ce bruit vient de l’arrondi calculé sur Pi, si on ajuste la virgule de Pi comme ceci :
# Frequence du signal
Sf0 = 2
f0 = (Sf0 * Fs)/T
# Décalage en seconde:
retard = 5
#temps: 0 points de 0 à N-1
t = np.linspace(0, T, N)
# morlet wavelet
y = np.cos(2*np.pi*f0*t)*np.exp(-np.power(t-retard,2)/2)
YTYPE="S1.15"
ysint = Fxp(y, dtype=YTYPE)
DTYPE="S8.8"
D2TYPE="S16.16"
fixpi = Fxp(np.pi, dtype="U3.13")
# transformée de fourrier
freqs_real = np.array([])
freqs_img = np.array([])
for k in range(N):
listreal = []
listimg = []
for n in range(N):
angle = Fxp(2*fixpi*Fxp(k*n, dtype="U16.0")/N, dtype=D2TYPE)
listreal.append(Fxp(y[n], dtype=YTYPE)*Fxp( np.cos(angle), dtype=YTYPE))
listimg.append (Fxp(y[n], dtype=YTYPE)*Fxp(-np.sin(angle), dtype=YTYPE))
xkreal = Fxp(np.array(listreal).sum(), dtype=DTYPE)
xkimg = Fxp(np.array(listimg ).sum(), dtype=DTYPE)
print(f"Freq {k}/{Fs} ({k*T/N}) -> {np.sqrt(xkreal*xkreal + xkimg*xkimg)})")
freqs_real = np.append(freqs_real, xkreal)
freqs_img = np.append(freqs_img, xkimg)
fourrier_power = Fxp(Fxp(freqs_img*freqs_img, dtype=DTYPE) + Fxp(freqs_real*freqs_real, dtype=DTYPE), dtype=DTYPE)
fourrier_module = Fxp((2/N)*Fxp(np.sqrt(fourrier_power), dtype=DTYPE), dtype=DTYPE)
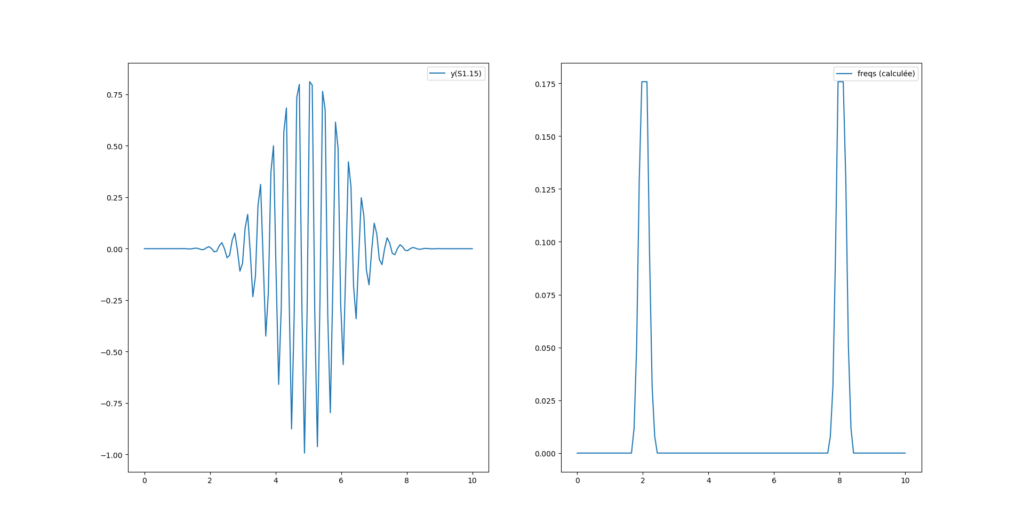
Par contre on a un décalage de fréquence avec la fonction magnitude_spectrum() de pylab :
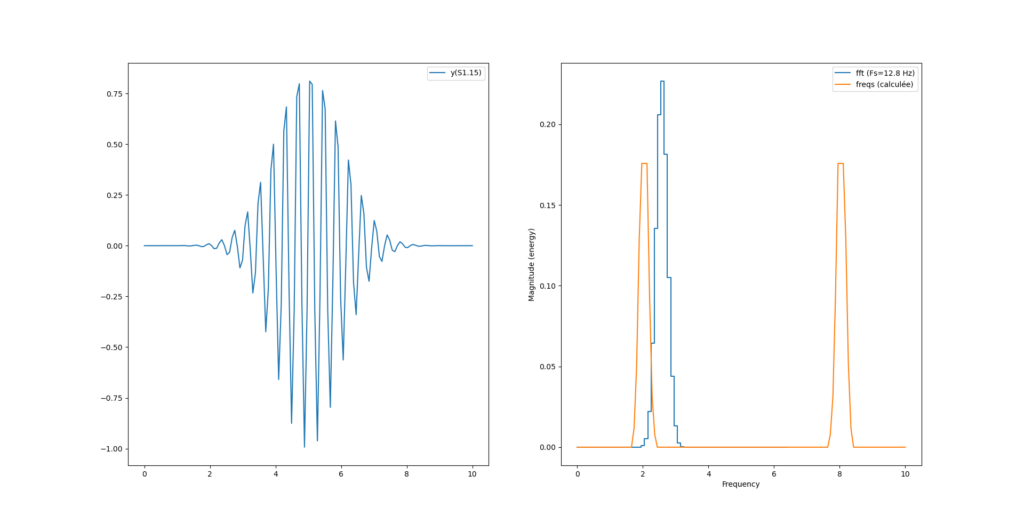
Ce décalage provient de l’axe des x qui n’est pas le même pour le calcul de python et le calcul maison. En effet, notre calcul «à la main» s’étend sur tout l’espace «de nyquist» (0 à N-1) alors que la fonction magnitude_spectrum() n’affiche le spectre que sur la moitée.
Pour recentrer tout ça on peut simplement récupérer la table des fréquences fournie par magnitude_spectrum() et l’utiliser comme axe des x dans l’affichage de notre spectre :
#...
magnitude, freqs, _ = ax[1].magnitude_spectrum(y, Fs=N/T, ds="steps-mid", label=f"fft (Fs={Fs} Hz)")
#...
ax[1].plot(freqs, fourrier_module[:len(freqs)], label = "freqs (calculée)")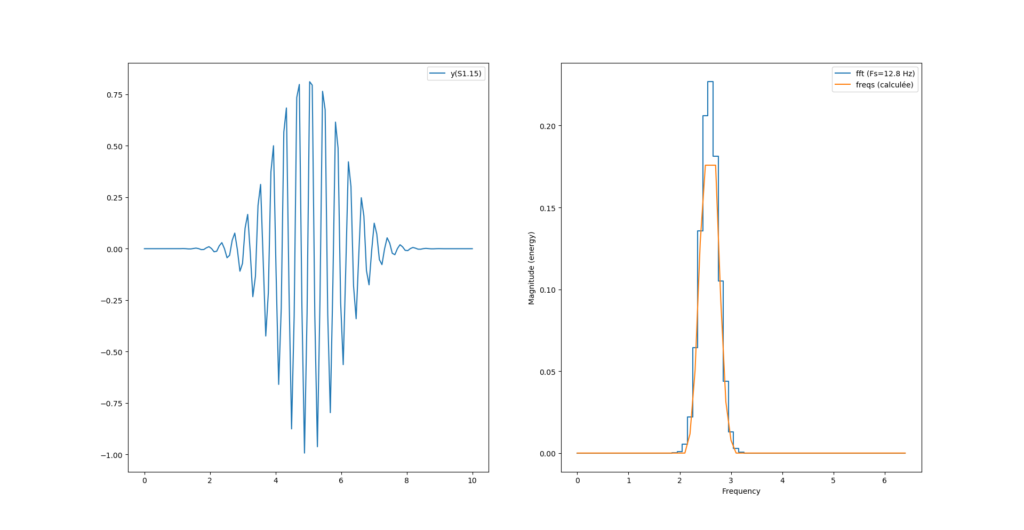
Et nous obtenons la bonne fréquence pour les deux modes de calculs. Reste maintenant un problème de magnitude maximum, est-ce un problème d’arrondi de la virgule fixe ? Possible.
Ressources
Le code de cet article se trouve sur le dépôt github suivant.
Test d’une carte Gowin avec LiteX
Après avoir déballé le kit gowin proposé par trenz micro. Il faut trouver quelques chose à faire de plus avancé qu’un simple clignotement de LED. Pour le clignotement de LED et la prise en main des outils, le lecteur se référera à l’article Hackable 32.
Pourquoi ne pas tenter le Linux des FPGA, j’ai nommé LiteX (Prononcez Lahïtixe ) ? LiteX est un framework HDL basé sur Migen pour construire des systèmes matériel facilement en python.
LiteX inclut un langage de description matériel, mais également tous les outils permettant de faire des simulations, la synthèses et générer les bitstreams pour la plupart des FPGA du marché. Bien évidement, en ce qui concerne la synthèse et les bitstreams, LiteX pilote les outils propriétaires des constructeurs. Ce pilotage ne pose généralement pas trop de problème, car tous les outils constructeurs proposent des interfaces en ligne de commande.
La carte que nous allons tenter de faire fonctionner avec LiteX est donc la TEC0117-1 produite par Trenz electronic et munie d’un FPGA gowin .

D’après le wiki, la carte n’est pas encore officiellement supporté par LiteX puisqu’elle ne se trouve pas dans la liste du projet LiteX-Boards…
Pas dans le tableau de la documentation du moins, car en fouillant dans le code du projet, il semble qu’il y ait déjà un embryon de quelques chose ici. Voila qui est très engageant pour tester la carte.
Voyons donc voir les étapes nous permettant de construire un système avec LiteX.
Installation de LiteX
Le plus simple pour installer LiteX sur son ordinateur est d’aller suivre le guide officiel d’installation.
$ wget https://raw.githubusercontent.com/enjoy-digital/litex/master/litex_setup.py
$ chmod +x litex_setup.py
$ ./litex_setup.py init install --user (--user to install to user directory)Attention, si comme moi vous avez un pc qui commence à prendre sérieusement de l’âge, sachez que le script litex_setup.py va descendre beaucoup de projets annexes de LiteX. Ça va prendre quelques minutes.
On aura besoin également de gcc compilé pour RISC-V :
$ ./litex_setup.py gccIl faudra bien penser à l’exporter à chaque fois qu’on en aura besoin :
$ export PATH=$PATH:$(echo $PWD/riscv64-*/bin/)Construire le système pour TEC0117
Pour construire un système pour la carte il faut ensuite se rendre dans le répertoire contenant la carte puis lancer le script python correspondant:
$ export PATH=$PATH:$(echo $PWD/riscv64-*/bin/)
$ cd litex-boards/litex_boards/targets
$ python3 trenz_tec0117.pyPour synthétiser et générer le bitstream il faut d’abord ajouter le lien vers l’ide (1.9.7 minimum) de gowin :
$ export PATH=$PATH:/opt/gowin/1_9_7/IDE/bin/Puis lancer le build:
$ python litex-boards/litex_boards/targets/trenz_tec0117.py --build
INFO:SoC: __ _ __ _ __
INFO:SoC: / / (_) /____ | |/_/
INFO:SoC: / /__/ / __/ -_)> <
INFO:SoC: /____/_/\__/\__/_/|_|
INFO:SoC: Build your hardware, easily!
INFO:SoC:--------------------------------------------------------------------------------
...
Running timing analysis......
[95%] Timing analysis completed
Bitstream generation in progress......
Bitstream generation completed
Running power analysis......
[100%] Power analysis completed
Generate file "/home/fabienm/myapp/litex/build/trenz_tec0117/gateware/impl/pnr/project.power.html" completed
Generate file "/home/fabienm/myapp/litex/build/trenz_tec0117/gateware/impl/pnr/project.pin.html" completed
Generate file "/home/fabienm/myapp/litex/build/trenz_tec0117/gateware/impl/pnr/project.rpt.html" completed
Generate file "/home/fabienm/myapp/litex/build/trenz_tec0117/gateware/impl/pnr/project.rpt.txt" completed
Generate file "/home/fabienm/myapp/litex/build/trenz_tec0117/gateware/impl/pnr/project.tr.html" completed
Fri Jul 9 13:18:07 2021
Le bitstream généré au format *.fs se trouve ensuite dans le répertoire
./build/trenz_tec0117/gateware/impl/pnr/project.fsOn pourra configurer le FPGA directement avec openFPGALoader :
$ openFPGALoader ./build/trenz_tec0117/gateware/impl/pnr/project.fs
Parse ./build/trenz_tec0117/gateware/impl/pnr/project.fs:
checksum 0x15d3
Done
erase SRAM Done
Flash SRAM: [==================================================] 100.000000%
Done
SRAM Flash: Success
Ou avec la bonne option litex (qui fait appel à openFPGALoader de toute manière):
$ python3 ../litex-boards/litex_boards/targets/trenz_tec0117.py --load
INFO:SoC: __ _ __ _ __
INFO:SoC: / / (_) /____ | |/_/
INFO:SoC: / /__/ / __/ -_)> <
INFO:SoC: /____/_/\__/\__/_/|_|
INFO:SoC: Build your hardware, easily!
INFO:SoC:--------------------------------------------------------------------------------
INFO:SoC:Creating SoC... (2021-07-12 19:05:10)
INFO:SoC:--------------------------------------------------------------------------------
INFO:SoC:FPGA device : GW1NR-LV9QN88C6/I5.
INFO:SoC:System clock: 25.00MHz.
INFO:SoCBusHandler:Creating Bus Handler...
...
INFO:SoC:Initializing ROM rom with contents (Size: 0x51cc).
INFO:SoC:Auto-Resizing ROM rom from 0x6000 to 0x51cc.
Parse /home/user/myapp/litex/myapp/build/trenz_tec0117/gateware/impl/pnr/project.fs:
checksum 0xa3a3
Done
erase SRAM Done
Flash SRAM: [==================================================] 100.000000%
Done
SRAM Flash: Success
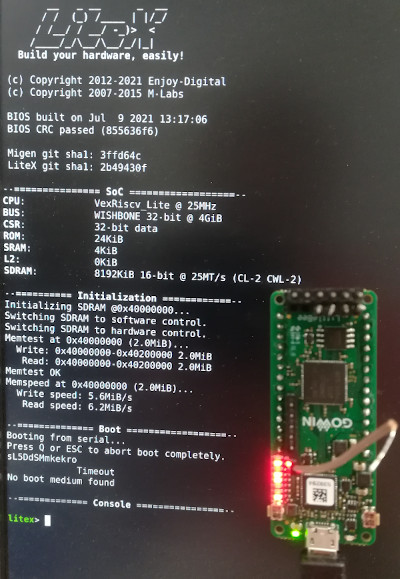
La confirmation de la bonne configuration est donnée par le message de la console, mais également par le chenillard de LED rouge.
Console litex>
Le convertisseur USB-uart de la carte possède deux interfaces ttyUSB, la première vient d’être utilisée par openFPGALoader pour charger le bitstream, la seconde permet de se connecter à la console litex :
$ screen /dev/ttyUSB1 115200
litex> reboot
__ _ __ _ __
/ / (_) /____ | |/_/
/ /__/ / __/ -_)> <
/____/_/\__/\__/_/|_|
Build your hardware, easily!
(c) Copyright 2012-2021 Enjoy-Digital
(c) Copyright 2007-2015 M-Labs
BIOS built on Jul 9 2021 13:17:06
BIOS CRC passed (855636f6)
Migen git sha1: 3ffd64c
LiteX git sha1: 2b49430f
--=============== SoC ==================--
CPU: VexRiscv_Lite @ 25MHz
BUS: WISHBONE 32-bit @ 4GiB
CSR: 32-bit data
ROM: 24KiB
SRAM: 4KiB
L2: 0KiB
SDRAM: 8192KiB 16-bit @ 25MT/s (CL-2 CWL-2)
--========== Initialization ============--
Initializing SDRAM @0x40000000...
Switching SDRAM to software control.
Switching SDRAM to hardware control.
Memtest at 0x40000000 (2.0MiB)...
Write: 0x40000000-0x40200000 2.0MiB
Read: 0x40000000-0x40200000 2.0MiB
Memtest OK
Memspeed at 0x40000000 (2.0MiB)...
Write speed: 5.6MiB/s
Read speed: 6.2MiB/s
--============== Boot ==================--
Booting from serial...
Press Q or ESC to abort boot completely.
sL5DdSMmkekro
Timeout
No boot medium found
--============= Console ================--
litex>
La commande help nous donnes les commandes disponibles :
litex> help
LiteX BIOS, available commands:
leds - Set Leds value
flush_l2_cache - Flush L2 cache
flush_cpu_dcache - Flush CPU data cache
crc - Compute CRC32 of a part of the address space
ident - Identifier of the system
help - Print this help
serialboot - Boot from Serial (SFL)
reboot - Reboot
boot - Boot from Memory
mem_speed - Test memory speed
mem_test - Test memory access
mem_copy - Copy address space
mem_write - Write address space
mem_read - Read address space
mem_list - List available memory regions
sdram_test - Test SDRAM
Photo traditionnelle
Avec LiteX, une tradition «twitter» veux que l’on fasse une photo du kit démarrant LiteX avec la console démarrée.
Et voila \o/
L’entrée en matière est incroyablement facile et fait honneur au slogan «Build your hardware, easily!».
Nous regarderons dans de futur articles ce que l’on peut faire avec.
CocoTB 1.4.0, la maturité
[Dépêche publiée initialement sur LinuxFR]
C’est dans la soirée du 8 juillet que l’annonce est tombée : la version 1.4.0 de CocoTB est sortie. Cette nouvelle version est une belle évolution de Cocotb avec une bonne intégration dans le système de paquets de Python ainsi que l’abandon de la prise en charge de Python 2. On peut aujourd’hui dire que CocoTB est une alternative sérieuse pour écrire ses bancs de test HDL.
Sommaire
Mais qu’est‑ce que c’est ?
CocoTB est une bibliothèque de cosimulation permettant d’écrire (en Python) des bancs de test pour la simulation numérique HDL (Hardware Description Language). Historiquement, les deux langages de descriptions HDL que sont Verilog et VHDL embarquent tout le nécessaire pour écrire des stimuli permettant de tester le composant en simulation. Cela permet d’avoir un seul langage pour décrire le composant et le tester. Le simulateur exécutera tout cela sans problème.
Mais cela amène beaucoup de confusion entre la partie du langage utilisable pour la simulation uniquement et la partie « description du matériel ». Dans le cas de la partie « matériel » on parle alors de code « synthétisable ». Cette confusion entre du code synthétisable ou non est source de grandes frustrations au moment de passer à la synthèse. En effet, cette belle structure de données que l’on aura développée et testée aux petits oignons s’écroulera au moment de la synthèse quand on se rendra compte que le code n’est pas synthétisable. Il faudra tout reprendre.
Une des idées derrière CocoTB est donc de changer de langage pour la simulation, comme cela les choses sont claires : on utilise le VHDL ou Verilog pour la partie du composant qui est synthétisable, et on passe au Python pour le banc de test. Ce n’est pas le seul logiciel à proposer ce genre d’approche. Avec Verilator, par exemple, on va écrire toute la partie banc de test en C++ ou en SystemC. La partie synthétisable sera écrite en Verilog et convertie en un objet C++ par Verilator.
La seconde idée de CocoTB est de ne pas réinventer la roue en réécrivant un énième simulateur HDL. Ce qui évite également d’avoir à choisir son camp entre Verilog et VHDL ou les deux (simulation mixte). Non, CocoTB va se contenter de piloter les simulateurs disponibles sur le marché. Les simulateurs libres que sont GHDL, Icarus et Verilator sont naturellement pris en charge, même si dans le cas de Verilator c’est très récent. La plupart des simulateurs commerciaux le sont également, ce qui est un argument pour l’introduire dans son bureau d’étude. En effet, les managers sont en général moyennement chauds pour virer un logiciel acquis à grands frais. Et l’on peut continuer à profiter des interfaces proposées par notre simulateur habituel pour exécuter le simulateur, visionner les chronogrammes, faire de la couverture de tests, etc.
La version 1.4 de CocoTB introduit la gestion complète du simulateur Aldec Active HDL qui vient s’ajouter aux classiques de Cadence et de Mentor, Modelsim…
Les changements dans le code
Un gros changement initié depuis quelque versions déjà est l’utilisation du mot clef async en lieu et place du yield et du décorateur @coroutine. Python 3 gérant désormais l’asynchronisme, CocoTB l’utilise et le prend désormais complètement en charge. L’exemple donné dans le courriel de la publication est le suivant :
@cocotb.test()
async def my_first_test(dut):
"""Try accessing the design."""
dut._log.info("Running test!")
for cycle in range(10):
dut.clk <= 0
await Timer(1, units='ns')
dut.clk <= 1
await Timer(1, units='ns')
dut._log.info("Running test!")Qui se serait écrit comme cela dans « l’ancien système » :
@cocotb.test()
def my_first_test(dut):
"""Try accessing the design."""
dut._log.info("Running test!")
for cycle in range(10):
dut.clk <= 0
yield Timer(1, units='ns')
dut.clk <= 1
yield Timer(1, units='ns')
dut._log.info("Running test!")Cette écriture restant cependant valable.
Le gros avantage de cette nouvelle écriture est de ne plus avoir a réinventer la roue avec des décorateurs inutiles. Avec async et await, on utilise des interfaces intégrées à Python 3, ce qui évite tout un travail de gestion.
Installation
CocoTB est, depuis maintenant un certain temps, partie intégrante du système de gestion de paquets de Python pip. Et vous pouvez dès à présent l’installer sur votre système via la commande pip install :
$ python -m pip install cocotb
# Pour celles et ceux qui ont installé la version précédente n’oubliez pas le --upgrade
$ python -m pip install --upgrade cocotbEt on peut vérifier la version grâce à la commande cocotb-config suivante :
cocotb-config --version
1.4.0
En plus de votre composant écrit en VHDL ou Verilog, deux fichiers supplémentaires sont nécessaires pour tester avec CocoTB : le Makefile et le script Python de test proprement dit.
Avec cette nouvelle version, le Makefile a encore été simplifié puisqu’il n’est plus nécessaire d’intégrer les en‑têtes C++. Ces en‑têtes sont nécessaires pour compiler les interfaces VPI/VHPI/FLI qui permettent de piloter les simulateurs. On compile désormais cette partie à l’installation de CocoTB. Dans les précédentes version, cette compilation ce faisait à chaque fois que l’on relançait les tests.
Si l’on prend l’exemple de l’antirebond en Verilog du Blinking Led Project, nous avons le Makefile suivant :
SIM=icarus # Nom du simulateur
export COCOTB_REDUCED_LOG_FMT=1 # Pour avoir des traces de log qui rentre dans l’écran
VERILOG_SOURCES = $(PWD)/../src/button_deb.v # Inclusion des fichiers HDL
TOPLEVEL=button_deb # Nom de l’entité
MODULE=test_$(TOPLEVEL) # Nom du script Python de test
include $(shell cocotb-config --makefile)/Makefile.simL’exemple est un composant permettant de ne pas compter les rebonds d’un bouton comme des appuis successifs.
Le script de test en Python se trouve dans le dépôt Git du projet et se nomme test_buton_deb.py. Pour le lancer, il suffit de se rendre dans le répertoire blp/verilog/cocotb/ et de taper make :
$ make
[...]
0.00ns INFO Running test!
0.00ns INFO freq value : 95000 kHz
0.00ns INFO debounce value : 20 ms
0.00ns INFO Period clock value : 10000 ps
0.02ns INFO Reset completeUn fichier de traces (chronogrammes) button_deb.vcd au format VCD est créé. Il peut être visionné en « temps réel » alors même que la simulation n’est pas terminée, grâce au visualiseur gtkwave :
$ gtkwave button_deb.vcd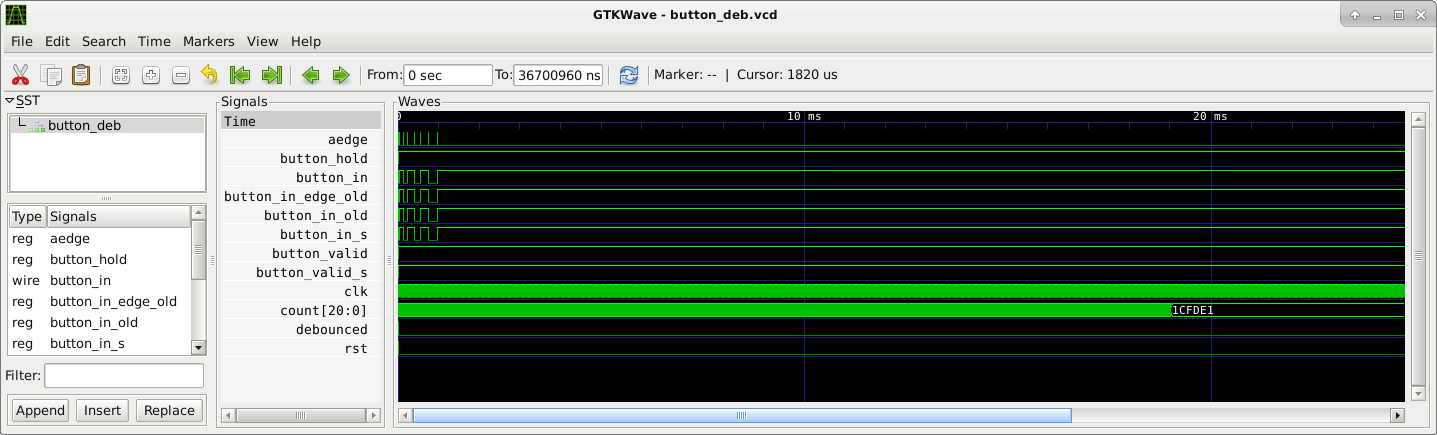
Une organisation qui tourne
Le projet CocoTB est chapeauté par la FOSSi foundation qui fournit le « chef de projet » Philipp Wagner ainsi que des moyens financiers pour faire tourner des machines virtuelles de tests ainsi que pour payer les licences des simulateurs commerciaux.
Les statistiques de modification de cette version sont les suivantes :
- 346 fichiers modifiés, 14 012 insertions (+), 10 356 suppressions (−) ;
- 554 commits ;
- 31 contributeurs ;
- 2 nouveaux mainteneurs : Colin Marquardt et Kaleb Barrett.
Ces chiffres montrent que CocoTB est un projet qui fédère désormais une grosse communauté. C’est un projet mature qui compte dans le paysage des logiciels libres pour le matériel (FPGA et ASIC).
Test your Chisel design in python with CocoTB
Chisel is a hardware description language embedded in Scala language. Compared to VHDL/Verilog Chisel it’s a high-level language. With Chisel it’s easier to parametrize and to abstract your hardware. It’s the language used for all SiFive RISC-V cores and for Google Edge TPU.
What’s great with chisel that it generate Verilog sources for synthesis. And we can use this Verilog generated design for simulation or formal prove.
Simulation can be done in Scala with chisel.testers. But this tester is mostly under development project for the moment. And there is no test library for common busses and devices like SPI, Wishbone, AXI, PWM, …
CocoTB is a cosimulation testbench framework written in Python. Main advantage of CocoTB is that you write your testbench stimulis in python language. Python is really comfortable programming language. The other advantage of using CocoTB is that there is a growing library of modules available to test devices like SPI, Wishbone, USB, uart, … And its easier to use a library than to reinvent the wheel.
Then, let’s write Chisel testbench with CocoTB !
As an example we will use the ChisNesPad project (yes, same as formal prove article).
The directory structure is following :
/
|-- build.sbt <- scala build configuration
|-- src/ <- all chisel sources
| |-- main/
| |-- scala/
| |-- chisnespad.scala <- Chisel module we will test
| |-- snespadled.scala <- "top" module to test with
| tang nano (gowin)
|-- formal/ <- formal directory
|-- platform/ <- some usefull files for synthesis with
| final platform (gowin).
|-- cocotb/ <- python cocotb tests
|-- chisnespad/ <- test for chisnespad core
| |-- Makefile <- makefile to compile and launch simulation
| |-- test_chisnespad.py <- cocotb stimulis
|-- snespadled/ <- test for «top» project that toggle leds
| when push buttons
|-- Makefile
|-- test_snespadled.pyTo launch tests we needs following dependencies :
- Icarus Verilog : for simulation
- Python 3: This example use python 3.7. It can be compiled and used with virtualenv
- sbt: The scala build system
- Chisel : The official website explain how to use it
- CocoTB: and of course it need CocoTB that can be installed with python (
python -m pip install cocotb) - cocotbify: python package included in repository chisverilogutil. Its used to inject some Verilog code in top module to generate VCD traces.
- fpgamacro: it’s a Chisel library used to instantiate some fpga-specific RawModule. In our case it’s for ResetGen block.
- gtkwave: VCD waveforms viewer.
Once all dependencies installed we can clone the chisNesPad project :
$ git clone https://github.com/Martoni/chisNesPad.gitThen launch simulation :
$ cd chisNesPad/cocotb/chisnespad/
$ make
make[1]: Entering directory '/home/fabien/myapp/chisNesPad/cocotb/chisnespad'
[...] lots of compilation lines [...]
/myapp/chisNesPad/cocotb/chisnespad/build/libs/x86_64:/usr/local/lib:/usr/local/lib:/usr/local/lib:/usr/local/lib:/usr/local/lib MODULE=test_chisnespad \
TESTCASE= TOPLEVEL=ChisNesPad TOPLEVEL_LANG=verilog COCOTB_SIM=1 \
/usr/local/bin/vvp -M /home/fabien/myapp/chisNesPad/cocotb/chisnespad/build/libs/x86_64 -m gpivpi sim_build/sim.vvp
-.--ns INFO cocotb.gpi gpi_embed.c:103 in embed_init_python Using virtualenv at /home/fabien/pyenv/pyenv37/bin/python.
-.--ns INFO cocotb.gpi GpiCommon.cpp:91 in gpi_print_registered_impl VPI registered
0.00ns INFO Running tests with Cocotb v1.2.0 from /home/fabien/pyenv/pyenv37/lib/python3.7/site-packages
0.00ns INFO Seeding Python random module with 1583180134
0.00ns INFO Found test test_chisnespad.always_ready
0.00ns INFO Found test test_chisnespad.double_test
0.00ns INFO Found test test_chisnespad.simple_test
0.00ns INFO Running test 1/3: always_ready
0.00ns INFO Starting test: "always_ready"
Description: None
VCD info: dumpfile ChisNesPad.vcd opened for output.
401300.00ns INFO Test Passed: always_ready
401300.00ns INFO Running test 2/3: double_test
401300.00ns INFO Starting test: "double_test"
Description: None
436000.00ns INFO Value read CAFE
470420.00ns INFO Value read DECA
471440.00ns INFO Test Passed: double_test
471440.00ns INFO Running test 3/3: simple_test
471440.00ns INFO Starting test: "simple_test"
Description: None
506140.00ns INFO Value read CAFE
507160.00ns INFO Test Passed: simple_test
507160.00ns INFO Passed 3 tests (0 skipped)
507160.00ns INFO *************************************************************************
** TEST PASS/FAIL SIM TIME(NS) REAL TIME(S) RATIO(NS/S) **
*************************************************************************
** test_chisnespad.always_ready PASS 401300.00 2.78 144519.92 **
** test_chisnespad.double_test PASS 70140.00 0.49 143736.56 **
** test_chisnespad.simple_test PASS 35720.00 0.25 144120.85 **
**************************************************************************************
507160.00ns INFO *************************************************************************************
** ERRORS : 0 **
*************************************************************************************
** SIM TIME : 507160.00 NS **
** REAL TIME : 3.52 S **
** SIM / REAL TIME : 144276.59 NS/S **
*************************************************************************************
507160.00ns INFO Shutting down...
make[1]: Leaving directory '/home/fabien/myapp/chisNesPad/cocotb/chisnespad'
(Note : I can’t find how to change width of code text in this #*/% wordpress )
And we can see wave form with gtkwave:
$ gtkwave ChisNesPad.vcd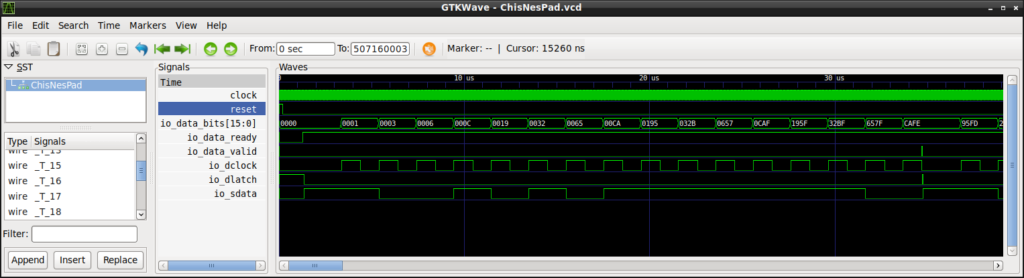
Let’s see what happen
All commands are described in the Makefile in directory chisNesPad/cocotb/chisnespad/.
Chisel Module
The Chisel Module we test here is in directory src/main/scala/chisnespad/ and is named chisnespad.scala with following interfaces :
class ChisNesPad (val mainClockFreq: Int = 100,
val clockFreq: Int = 1,
val regLen: Int = 16) extends Module {
val io = IO(new Bundle{
/* SNES Pinout */
val dclock = Output(Bool())
val dlatch = Output(Bool())
val sdata = Input(Bool())
/* read/valid output */
val data = Decoupled(Output(UInt(16.W)))
})
//...
}The scala verilog generator driver is given at the end of file :
object ChisNesPad extends App {
println("Generating Verilog sources for ChisNesPad Module")
chisel3.Driver.execute(Array[String](), () => new ChisNesPad)
}This object will be called by SBT following command:
$ sbt "runMain chisnespad.ChisNesPad"Generated Verilog
This will generate the Verilog file named ChisNesPad.v in root directory. With following interfaces :
module ChisNesPad(
input clock,
input reset,
output io_dclock,
output io_dlatch,
input io_sdata,
input io_data_ready,
output io_data_valid,
output [15:0] io_data_bits
);
//...
endmoduleAs we can see, all bundled ports are kept but with little modification : dot ‘.’ are replaced by underscore ‘_’. clock and reset has been added and we can retrieve our decoupled signal io.data.{ready, valid, bits} -> io_data_{ready, valid, bits} .
CocoTB testbench
With these changes in mind, we can read/write our chisel ports signals with CocoTB.
CocoTB tests are described in file test_chisnespad.py. This file describe a class to store all method and data for testing ChisNesPad Module then list cocotb test function :
# main class for all test
class ChisNesPadTest(object):
"""
"""
LOGLEVEL = logging.INFO
PERIOD = (20, "ns")
SUPER_NES_LEN = 16
NES_LEN = 8
def __init__(self, dut, reg_init_value=0xcafe, reg_len=16):
if sys.version_info[0] < 3:
raise Exception("Must be using Python 3")
self._dut = dut
#...
# all tests
@cocotb.test()
def simple_test(dut):
cnpt = ChisNesPadTest(dut)
yield cnpt.reset()
yield Timer(1, units="us")
dut.io_data_ready <= 1
#...
@cocotb.test()#skip=True)
def double_test(dut):
cnpt = ChisNesPadTest(dut)
yield cnpt.reset()
#...
@cocotb.test()
def always_ready(dut):
cnpt = ChisNesPadTest(dut)
yield cnpt.reset()
#...Here we see tree tests decorated with @cocotb.test(). The our module ChisNesPad is the Device Under Test (DUT) and is passed in test function arguments : dut.
To access input/output ports we just have to use dot on our dut object.
- set io.data.ready to logic level ‘1’ :
dut.io_data_ready <= 1- read io.data.bits
vread = int(dut.io_data_bits)- We can also read register under the module or a submodule :
countvalue = int(dut.countReg)It’s also possible to write register under the module, but be careful of the race condition when you doing that. It can be re-written by simulation with 0-delay.
Get Waveform
All tests can be done with procedure describe above. But with Icarus as simulator we don’t get the waveforms.
It’s not easy to develop HDL without any waveform. To get waveform we can use another simulator that will generate the traces (mainly in VCD format) but Icarus is mature and free then it’s cheaper to use it.
The solution given in CocoTB documentation is to add following verilog code in top module :
`ifdef COCOTB_SIM
initial begin
$dumpfile ("ChisNesPad.vcd");
$dumpvars (0, ChisNesPad);
#1;
end
`endifWith this $dumpX() function we will records all signals under the file named ChisNesPad.vcd. If we had to add this code by hand each time we re-generate verilog from Chisel module, it would quickly become painful.
That why we use the tool cocotbify, included in package chisverilogutils.
$ cocotbify
Usages:
cocotbify.py [options]
-h, --help print this help
-v, --verilog verilog filename to modify (filename is used
as module name)
-o, --output filename output filenameThis tool will take a verilog source as input and generate an output with dumpvars code added for cocotb. In the example makefile the output name will be ChisNesPadCocotb.v. This file will be used by CocoTB and Icarus for simulation. VCD file can then be view with gtkwave:
$ gtkwave ChisNesPad.vcd
Conclusion
As we can see, it’s perfectly possible to use CocoTB framework for testing Chisel components. CocoTB has more library test modules available than chisel.tester and we can code in Python. Python is used by lots of peoples through the world and is less scary than Scala or SystemVerilog for hardware engineers that develop digital hardware.
Cocotb Tips
Some tips for python HDL test module Cocotb.
Read and Write signal
Write:
clk.value = 1
dut.input_signal <= 12
dut.sub_block.memory.array[4] <= 2Read:
count = dut.counter.value
print(count.binstr)
print(count.integer)
print(count.n_bits)
print(int(dut.counter))See it under the official documentation.
Yielding a coroutine in a select list fashion
Question asked on stackoverflow.
Using latest python version with virtualenv
If you compile python yourself, don’t forget to add option --enable-shared at configure time (./configure --enable-shared)
$ virtualenv --python=/usr/local/bin/python3.7 ~/envp37
$ source ~/envp37/bin/activate
$ python -m pip install cocotbDo not forget to re-source your environnement each time you open a new terminal :
$ source ~/envp37/bin/activateLogging messages and main test class template
This is a template for declaring a class used for test in function @cocotb.test() :
import logging
from cocotb import SimLog
...
class MyDUTNameTest(object):
""" Test class for MyDUTName"""
LOGLEVEL = logging.INFO
# clock frequency is 50Mhz
PERIOD = (20, "ns")
def __init__(self):
if sys.version_info[0] < 3: # because python 2.7 is obsolete
raise Exception("Must be using Python 3")
self._dut = dut
self.log = SimLog("RmiiDebug.{}".format(self.__class__.__name__))
self.log.setLevel(self.LOGLEVEL)
self._dut._log.setLevel(self.LOGLEVEL)
self.clock = Clock(self._dut.clock, self.PERIOD[0], self.PERIOD[1])
self._clock_thread = cocotb.fork(self.clock.start())
# ....
@cocotb.test()
def my_test(dut):
mdutn = MyDUTNameTest()
mdutn.log.info("Launching my test")